O que é elipse? Uma figura geométrica?

Uma elipse é uma figura geométrica plana obtida pela intersecção entre um plano e um cone. É por isso que essa figura é chamada de cônica, assim como a circunferência, a parábola e a hipérbole. A figura a seguir é um exemplo de elipse e demonstra a diferença entre a representação geométrica dessa figura e a circunferência.

Na figura acima, os pontos F₁ e F₂ são focos da elipse, e a distância entre eles é definida como 2c.

Tópicos deste artigo

• 1 - Definição formal da elipse
• 2 - Elementos da elipse
• 3 - Equações reduzidas da elipse

Definição formal da elipse

Dados os pontos F₁ e F₂, com a distância 2c entre eles, a elipse é o conjunto dos pontos P em que é válida a seguinte igualdade:

d_PF1 + d_PF2 = 2a

Em outras palavras, a elipse é o conjunto de pontos no qual a soma das distâncias até cada um dos focos é igual à constante 2a. Assim, podemos dizer que P é um ponto pertencente a uma elipse se a soma das distâncias de P até cada um dos focos for igual a 2a.

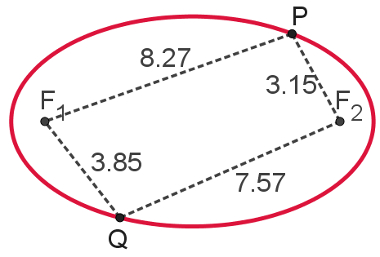
A imagem a seguir ilustra essa definição. Observe que a soma das distâncias entre P e os focos da elipse é igual à soma das distâncias do ponto Q até o foco da elipse. Por isso, P e Q pertencem a essa elipse.

Note que o comprimento 2a é sempre maior do que o comprimento 2c.

Elementos da elipse

A seguir, confira uma lista com os principais elementos da elipse e uma breve definição de cada um deles.

Focos: nas imagens presentes neste artigo, os focos são os pontos F₁ e F₂. São pontos-chave em que as distâncias devem ser avaliadas para saber se um ponto pertence ou não pertence à elipse.

Centro: dados os focos F₁ e F₂, o centro da elipse é o ponto médio do segmento F₁F₂ cujas extremidades são os focos.

Eixo maior: na imagem abaixo, o eixo maior é o segmento A₁A₂. Suas extremidades são pontos que pertencem à intersecção entre a elipse e a reta que contém os focos. A medida desse eixo é igual a 2a, mesmo comprimento da soma das distâncias entre um ponto qualquer da elipse e seus focos.

Eixo menor: na imagem abaixo, o eixo menor é o segmento B₁B₂. Suas extremidades são pontos que pertencem à intersecção entre a elipse e a reta perpendicular ao eixo maior. O comprimento desse eixo é igual a 2b, em que b é a distância entre o centro da elipse e o ponto B₁.

Distância focal: Distância entre os focos da elipse e é sempre igual a 2c.

Excentricidade: é a seguinte razão:

c
a

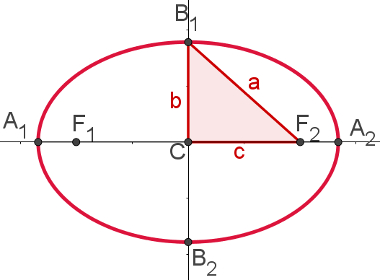
A imagem a seguir ilustra alguns dos elementos da elipse e os comprimentos que representam as medidas “a”, “b” e “c”, em que se pode observar a relação de Pitágoras: a² = b² + c².

Equações reduzidas da elipse

A primeira equação reduzida da elipse é usada no caso em que os focos dessa figura estão sobre o eixo x e o centro da elipse está sobre a origem do plano cartesiano:

  x²  +   y²  = 1
a²       b²      

A segunda equação reduzida da elipse é usada no caso em que os focos dessa figura estão sobre o eixo y e o centro está sobre a origem do plano cartesiano:

  y²  +   x² = 1
a²       b²     

Por Luiz Paulo Moreira
Graduado em Matemática