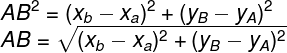O que é geometria analítica?

Geometria analítica é o ramo da Matemática que estuda a geometria plana e espacial por meio de processos algébricos. Isso significa que toda a geometria euclidiana pode ser estudada por meio dos procedimentos estabelecidos pela geometria analítica. Dessa forma, ela cria para a geometria euclidiana novas técnicas que podem ser usadas para a demonstração de teoremas, criação e demonstração de propriedades etc.

Tópicos deste artigo

• 1 - As bases da geometria analítica
• 2 - Distância entre dois pontos

As bases da geometria analítica

O primeiro passo a ser dado para estudar a geometria euclidiana (plana e espacial), por meio de processos algébricos, é criar mecanismos para introduzir a álgebra nessa disciplina. Para tanto, utiliza-se a reta numérica para que pontos específicos representem números reais únicos. Assim, a distância entre um ponto qualquer da reta numérica e sua origem é um número real relativo à localização desse ponto na reta. Esse número real pode ser chamado de coordenada do ponto.

Tomando duas retas perpendiculares que se encontram na origem, é possível encontrar a localização de qualquer ponto dentro do plano formado por elas utilizando um par ordenado, que é o conjunto de duas coordenadas, cada uma relativa a uma das retas que definiram esse plano. O mesmo vale para três retas ortogonais que se encontram em suas origens: formam um espaço tridimensional, no qual é possível determinar a localização de qualquer ponto por meio de ternos ordenados.

O plano descrito acima, formado por duas retas perpendiculares que se encontram em suas origens, é chamado de plano cartesiano. Esse plano é o primeiro espaço no qual estudamos a geometria analítica.

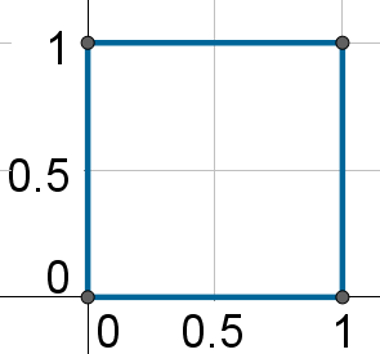
Tanto na reta quanto no plano e no espaço, é possível definir a distância entre dois pontos. Essa distância fica definida como o comprimento do segmento de reta que os liga. Imagine agora um plano cartesiano e nele os pontos A(0, 0), B(0, 1), C(1, 1) e D(1, 0). Esses pontos formam um quadrado, e isso pode ser observado na figura a seguir:

Os ângulos internos da figura formada pelos pontos acima são todos retos, e a distância entre dois pontos consecutivos é sempre igual a 1 unidade.

Portanto, o conceito de distância entre dois pontos é um dos mais importantes de toda a geometria analítica. Esse conceito permite desde a definição de alguns elementos, como a de comprimento do segmento de reta, até a demonstração de importantes teoremas da Geometria.

Distância entre dois pontos

Como dito antes, o conceito de distância entre dois pontos é um dos mais importantes da geometria analítica. No quadrado da imagem anterior, as distâncias mostradas eram segmentos de reta paralelos ao eixo x ou ao eixo y, mas é possível calcular a distância entre quaisquer dois pontos em um plano cartesiano.

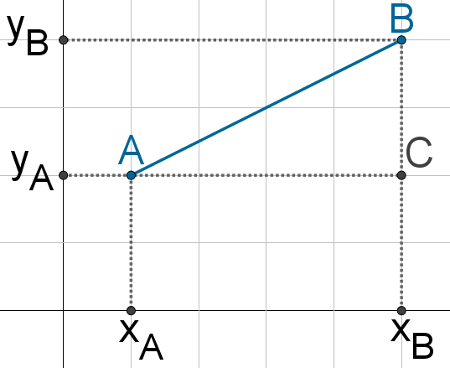
Para tanto, vamos recorrer à álgebra. Dados os pontos A(x_A, y_A) e B(x_B, y_B), sabemos que a distância entre esses dois pontos é o comprimento do segmento AB. Observe esse segmento na figura a seguir:

As projeções dos pontos A e B sobre os eixos formam o triângulo ABC, que é retângulo em C. Perceba que o comprimento do segmento AC é igual a x_B – x_A, e que o comprimento do segmento BC é dado por y_B – y_A. O comprimento do segmento AB pode ser obtido por meio de teorema de Pitágoras:

Esse resultado obtido é a fórmula para o cálculo da distância entre dois pontos no plano.