Neste artigo separamos três conceitos básicos que geralmente estão presentes tanto em Matemática quanto em Física e Química nas provas do Enem. Exercícios envolvendo exclusivamente eles não apresentam dificuldade alguma para serem resolvidos, por isso, são menos frequentes no exame. Esses conceitos normalmente aparecem de forma indireta. Veja quais são eles:
1º: Jogo de sinais
O conjunto dos números inteiros é formado por todos os números inteiros positivos, negativos e pelo zero. Em virtude da presença de números negativos, que soma regras à adição e à multiplicação, as operações básicas entre eles apresentam algumas diferenças que carecem de adaptação. Observe:
→ Jogos de sinais: Soma de números inteiros
Ao somar dois números inteiros, observe seus sinais para escolher entre as alternativas:
1) Sinais iguais
Some os números e conserve o sinal para o resultado. Por exemplo:
a) (– 16) + (– 44) = – 60
b) (+ 7) + (+ 13) = 20
Note que é possível escrever as mesmas expressões numéricas acima de forma reduzida:
a) – 16 – 44 = – 60
b) 7 + 13 = 20
Resumindo: Ao somar dois números negativos, o resultado será negativo. Ao somar dois números positivos, o resultado será positivo.
2) Sinais diferentes
Subtraia os números e mantenha o sinal daquele que for maior em módulo, isto é, aquele que for maior independentemente do sinal. Por exemplo:
a) (+ 16) + (– 44) = – 28
b) (– 7) + (+ 13) = 6
Note que – 44 é menor que + 16 pelo simples fato de ser negativo. Contudo, ignorando os sinais, 44 é maior que 16. Logo, 44 é o maior em módulo e, por isso, seu sinal prevalece no resultado. Também é possível escrever as mesmas expressões numéricas acima na forma reduzida:
a) 16 – 44 = – 28
b) – 7 + 13 = 6
Resumindo: ao somar dois números cujos sinais são diferentes, subtraia os números e mantenha para o resultado o sinal daquele que for maior em módulo.
As mesmas regras valem para expressões numéricas que envolvam mais do que dois números para serem somados, de modo que, para resolvê-las, basta somar seus termos dois a dois. Não é necessário falar em subtração, pois, a partir do conjunto dos números inteiros, a subtração é uma adição entre números com sinais diferentes.
Para mais informações e exemplos a respeito da soma, leia o texto Operações entre números inteiros.
→ Jogos de sinais: Multiplicação de números inteiros
As regras para os sinais na multiplicação de números inteiros são as mesmas para a divisão. Confira:
1) Sinais iguais
Quando os sinais forem iguais em uma multiplicação, o resultado sempre será positivo. Por exemplo:
a) (+ 16)·(+ 4) = + 64
b) (– 8)·(– 8) = + 64
Repare que, na multiplicação de dois números negativos, o resultado será positivo porque esses dois números possuem sinais iguais. Aconselhamos o uso de parênteses sempre para a multiplicação.
2) Sinais diferentes
Quando os sinais forem diferentes em uma multiplicação, o resultado sempre será negativo. Por exemplo:
a) 16·(– 2) = – 32
b) (– 7)·(+ 3) = – 21
As mesmas regras valem para a divisão. Para mais informações envolvendo multiplicação de números inteiros e jogo de sinais, leia o texto: Multiplicação de números inteiros.
2º: Equações
Como este texto trata de conceitos básicos, discutiremos definições e propriedades de equações do primeiro grau. Para resolver equações do segundo grau, sugerimos a leitura do texto Fórmula de Bháskara.
Para resolver uma equação, isto é, encontrar o valor numérico da incógnita, é necessário cumprir os três passos seguintes:
1) Colocar todos os termos que possuem incógnita no primeiro membro;
2) Colocar todos os termos que não possuem incógnita no segundo membro;
3) Realizar os cálculos resultantes;
4) Isolar a incógnita.
Por exemplo:
12x – 4 = 6x + 20
Passos 1 e 2: 12x – 6x = 20 + 4
Passo 3: 6x = 24
Passo 4: x = 24
6
x = 4
Para mais informações sobre solução de equações e alguns exemplos, leia os textos:
1) Equação do 1º grau com uma incógnita
2) Problemas envolvendo o uso de equações
3) Introdução à equação do 1º grau
3º: Regra de três simples
A regra de três é assim conhecida por relacionar quatro valores referentes a duas grandezas, de modo que três deles sejam conhecidos. Ela funciona apenas para grandezas proporcionais, isto é, para aquela grandeza que varia proporcionalmente à variação de outra grandeza.
A grandeza Distância percorrida, por exemplo, é proporcional à grandeza Velocidade. Em um determinado período de tempo, quanto maior for a velocidade, maior será a distância percorrida.
Exemplo:
Digamos que um homem seja acostumado a ir ao trabalho por dentro da cidade a uma velocidade média de 40 km/h. Sabendo que o percurso casa-trabalho é de 20 km, quantos quilômetros ele alcançaria se estivesse a 110 km/h?
Note que as grandezas velocidade e distância percorrida são proporcionais. Obviamente, dentro do mesmo intervalo de tempo, esse homem alcançará uma distância muito maior andando a 110 km/h. Para descobrir essa distância, podemos montar a seguinte tabela:
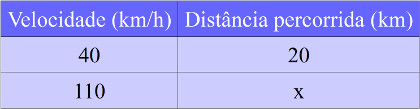
Agora, basta montar uma igualdade, seguindo a mesma posição dos elementos da tabela, e utilizar a regra “Produto dos extremos pelos meios”.
40 = 20
110 x
40x = 20·110
40x = 2200
x = 2200
40
x = 55
Para maiores informações, discussões e exemplos a respeito de regra de três simples e composta, consulte os textos:
b) Porcentagem utilizando regra de três
Para aprofundar os conhecimentos a respeito de proporcionalidade, que fundamenta a regra de três, leia os textos:
b) Proporcionalidade entre grandezas
Por Luiz Paulo Moreira
Graduado em Matemática
