Hoje apresentamos para você algumas dicas e macetes que podem fazer a diferença para aqueles que pretendem fazer o Enem. É sabido que o Exame contém muitas questões para serem resolvidas em poucas horas. Desse modo, quanto mais tempo o candidato economizar em questões mais fáceis, mais tempo terá para concentrar-se naquelas que precisam de um pouco mais de atenção.
A maioria das questões de Matemática e Física do Enem exige que o estudante tenha conhecimento de algum conteúdo específico e de outros conteúdos fundamentais que devem ser utilizados nas resoluções. Desse modo, não há dúvidas de que conteúdos como equações, jogo de sinais, adição, multiplicação e divisão, entre outros, caem em praticamente todas as questões de Matemática e Física do Enem.
Vamos às dicas?!
→ Jogo de sinais
Em vez de decorar todas as regras para multiplicação entre números positivos e negativos, por que não aprender a regra?
“Sinais iguais, resultado positivo”
Isso é o mesmo que dizer que, se os sinais forem diferentes, o resultado da multiplicação será negativo.
Cuidado! Essa regra só é valida para multiplicação. Nada de aplicá-la às somas e subtrações. A regra para a adição é diferente:
Com sinais iguais, some e conserve-os.
Com sinais diferentes, subtraia e mantenha o sinal do maior módulo.
Observe que módulo é quando o sinal é ignorado. Por exemplo, entre 8 e – 9, o número que tem maior módulo é o – 9, apesar de o 8 ser maior em um sentido geral.
→ Multiplicação por potência de 10
Na hora de multiplicar qualquer número por uma potência de 10, pense apenas na vírgula. O número de casas decimais que ela se deslocará para a direita é igual ao expoente da potência de 10 pelo qual o número está sendo multiplicado. Observe:
4,58·1000
4,58·103
4 580,0
Observe no exemplo acima que a vírgula deslocou-se três casas decimais. No caso da divisão por potência de 10, a vírgula deve deslocar-se para a esquerda.
O segundo caso é aquele em que não há vírgula. Para calcular esse tipo de multiplicação, basta colocar zeros no final do número. A quantidade de zeros é igual ao expoente da potência de 10. Observe:
458·1000000
458·107
4580000000
→ Multiplicação por múltiplo de 10
Quando os números multiplicados são múltiplos de 10, o procedimento é similar ao anterior. Contudo, separe os números em duas partes: início e zeros. Multiplique os números iniciais e coloque exatamente a mesma quantidade de zeros que eles possuem no resultado final. Exemplo:
2800·32000
28·32 = 896, logo:
2800·32000 = 89600000
Cuidado! Se houver zeros entre os números iniciais, eles não vão parar no final do resultado. Observe:
101·208
21008
→ Multiplicação pela propriedade distributiva
Unindo esse tópico ao anterior, com um pouco de treino, é possível realizar muitas divisões dificílimas “de cabeça”. Para utilizar a referida propriedade na multiplicação, decomponha um dos números em múltiplos de 10, multiplique todos os fatores obtidos pelo outro número e some os resultados. Observe:
325·22
325·(20 + 2)
É possível realizar esses cálculos “de cabeça”. Observe que utilizamos o tópico anterior para facilitar o cálculo:
6500 + 650
7150
Essa simplificação pode ser extremamente útil para não perder tempo com longas multiplicações no dia do Enem. Observe que transformamos uma multiplicação difícil em duas outras multiplicações fáceis que, somadas, dão o mesmo resultado.
→ Tabela trigonométrica
A tabela a seguir sempre é explorada em algumas questões de Trigonometria do Enem. Entretanto, poucas vezes os resultados presentes nela são dados no exercício. Por isso, é importante que o candidato a tenha em mente antes de se dirigir aos locais de prova.
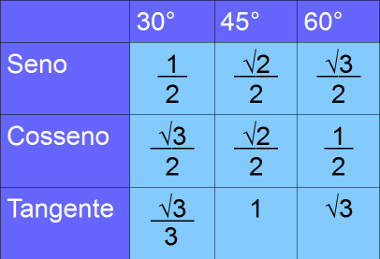
Para aprender essa tabela, sugerimos a seguinte música:
“Um, dois, três.
Três, dois, um...
Tudo sobre dois
Só não tem raiz o um.”
Note que essa música pode ser usada como passo a passo para construir essa tabela para os valores de seno e cosseno. Os valores de tangente podem ser obtidos dividindo-se seno por cosseno.
→ Adição de arcos
O seno da soma de dois ângulos não é obtido apenas com a soma desses ângulos e cálculo do valor de seno. Existem fórmulas para a adição de arcos. A mais recorrente delas é a que envolve seno. Para memorizá-la, podemos utilizar o início da Canção do Exílio, de Gonçalves Dias:
“Minha terra tem palmeiras
Onde canta o sabiá
Seno a, cosseno b
seno b, cosseno a”
Isso deve ser transcrito da seguinte maneira:
sen(a + b) = sena·cosb + senb·cosa
sen(a – b) = sena·cosb – senb·cosa
→ Juros simples
Muitas vezes aparecem problemas envolvendo juros simples no Enem. A fórmula para o cálculo de juros simples é a seguinte:
J = C·i·t
J = juros; C = capital; i = taxa e t = tempo.
Para memorizar essa fórmula, utilize o seguinte macete:
“Jota City”
Perceba que esse macete é justamente a pronúncia da fórmula, o que torna impossível esquecê-la. Observe também que a fórmula para juros compostos pode enquadrar-se em um macete parecido:
“M-ciity”
A fórmula para juros compostos é a seguinte:
M = C(1 + i)t
Observe que os juros compostos não são obtidos diretamente dessa fórmula, mas, sim, pela diferença entre Montante (M) e Capital (C):
M = C + J
J = M – C
Por Luiz Paulo Moreira
Graduado em Matemática




