Identidade entre Triângulos

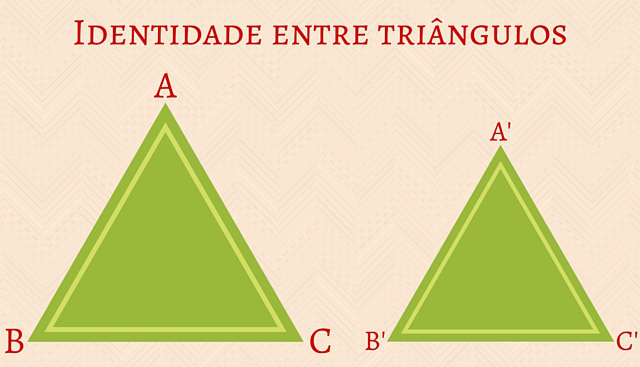
Dizemos que dois triângulos são semelhantes se, e somente se, os ângulos no mesmo posicionamento forem iguais e os lados correspondentes, proporcionais. Observe:

 Os ângulos A, B e C são, de forma posicional, iguais aos ângulos A’, B’ e C’.

Os lados a, b e c são iguais de maneira proporcional aos ângulos a’, b’ e c’:
 , em que k é uma constante de proporcionalidade.

Na determinação da identidade entre triângulos estabelecemos uma propriedade conhecida como Teorema Fundamental da Semelhança, que diz:

Se em um triângulo for traçado um segmento de reta paralelo a um dos lados e que intersecta os outros dois lados em pontos diferentes, temos que será determinado um segundo triângulo semelhante ao primeiro.

Observe a figura a seguir:

Observe a semelhança entre os lados:

AB proporcional a AE
AC proporcional a AD
BC proporcional a DE

Essa relação é determinada de acordo com o Teorema de Tales, que enuncia:

Retas paralelas cortadas por retas transversais formam segmentos proporcionais.

Exemplo

De acordo com as propriedades da semelhança e com o Teorema de Tales, determinaremos o valor de x na figura a seguir:

Por Marcos Noé
Graduado em Matemática
Equipe Brasil Escola

Triângulo - Matemática - Brasil Escola