O que são polígonos convexos e regulares?

Polígonos convexos e regulares são classificações dessas figuras geométricas em relação à sua forma. Para melhor compreensão desses conceitos classificatórios, é necessário conhecer alguns outros conceitos básicos acerca dos polígonos.

Um polígono é uma região do plano formada pela união de uma linha fechada – que, por sua vez, é formada por segmentos de reta chamados de lados – e todos os pontos interiores a essa linha.

São exemplos de polígonos os triângulos, os quadrados, os retângulos e os paralelogramos. Além deles, todas as figuras geométricas que seguem o padrão de construção desses exemplos também são polígonos, como é o caso dos pentágonos, hexágonos, heptágonos etc.

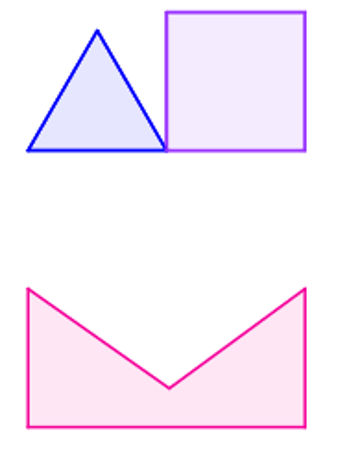
Exemplos de polígonos

Não são polígonos, portanto, figuras que apresentam em um de seus lados, no lugar de um segmento de reta, uma curva qualquer ou que dois de seus lados cruzam-se.

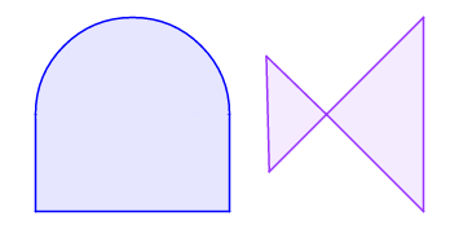
Exemplos de não polígonos

Um polígono é convexo quando, dados dois pontos A e B quaisquer em seu interior, é impossível encontrar um segmento de reta AB com pelo menos um ponto no exterior do polígono, ou seja, tomando dois pontos A e B dentro de um polígono, se o segmento AB sempre estiver inteiramente no interior do polígono, independentemente da localização dos pontos A e B, esse polígono será convexo.

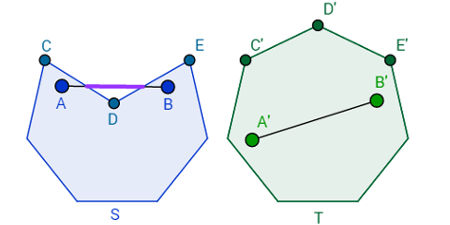
Exemplos de polígonos convexos e não convexos

Na imagem acima, observe que o polígono S possui uma espécie de “boca” entre os pontos C e E. Note também que o ponto D avança para o interior do polígono. Esse polígono não é convexo, fato que pode ser notado pela parte destacada do segmento AB. Essa parte está no exterior do polígono, enquanto os pontos A e B são interiores a ele. Conforme a definição anterior, o polígono S não é um polígono convexo.

Em relação ao polígono T, qualquer localização observada para os pontos A' e B' gera um segmento de reta A'B' totalmente interior ao polígono. Portanto, o polígono T é convexo.

Polígonos regulares são polígonos convexos que possuem todos os lados congruentes e todos os ângulos internos também congruentes. É importante ressaltar que os ângulos e lados não precisam ter a mesma medida – afirmar que eles possuem a mesma medida sequer faz sentido. Então, a definição geralmente fala “lados congruentes e ângulos internos também congruentes” para evitar esse tipo de confusão.

Dessa forma, qualquer polígono em que todos os lados e ângulos possuem a mesma medida é chamado de polígono regular.

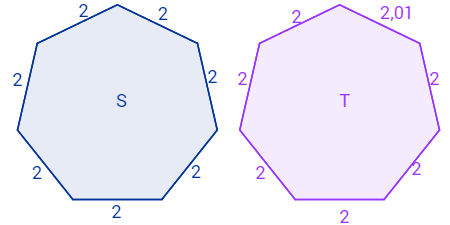
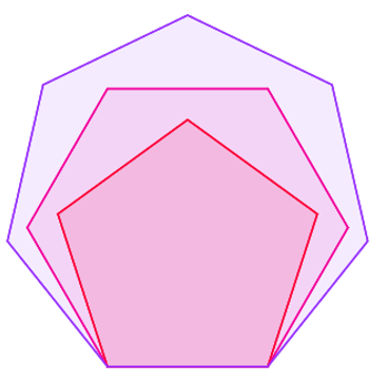
Exemplos de polígonos regulares e não regulares

Na imagem acima, o polígono S é regular por estar de acordo com a definição. Por outro lado, o polígono T não é regular. Apesar de a figura parecer um polígono regular, um dos lados desse polígono possui medida diferente da medida dos demais.

Um polígono qualquer possui os seguintes elementos:

1 – Lados: segmentos de reta constituintes do contorno de um polígono;

2 – Vértices: pontos de encontro entre os lados.

Um polígono convexo, além dos elementos citados acima, possui os seguintes elementos:

3 – Ângulos internos: ângulos formados por dois lados consecutivos na região interior do polígono.

4 – Ângulos externos: são formados por um lado e o prolongamento do lado consecutivo a ele. Dessa forma, a soma entre um ângulo interno e um ângulo externo pertencentes ao mesmo vértice é sempre igual a 180°.

5 – Diagonais: segmentos de reta que ligam dois vértices não consecutivos de um polígono.

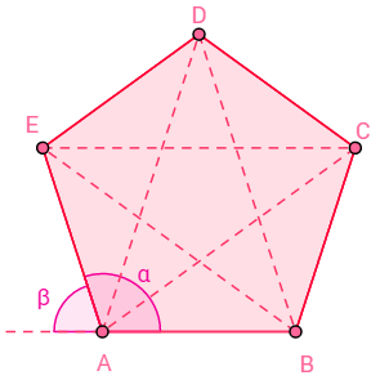
Exemplos dos elementos de um polígono convexo

Na imagem acima, os vértices são os pontos A, B, C, D e E. Os lados são AB, BC, CD, DE e EA. As diagonais são as linhas pontilhadas. No vértice A, α é o ângulo interno e β é o ângulo externo.

Por Luiz Paulo Moreira
Graduado em Matemática