O que é a condição de existência de um triângulo?

A condição de existência de um triângulo é um conjunto de relações entre as medidas de seus lados que possibilitam decidir se, com as medidas propostas, é possível construí-lo. Essa condição pode ser vista como uma propriedade e é conhecida como desigualdade triangular.

Condição de existência de um triângulo

Dados três segmentos de reta distintos, se a soma das medidas de dois deles é sempre maior que a medida do terceiro, então, eles podem formar um triângulo. Por exemplo, dados os segmentos AB = 16 cm, CD = 20 cm e EF = 30 cm, é possível usá-los para construir um triângulo, pois as somas abaixo são verdadeiras:

16 + 20 = 36 > 30

16 + 30 = 46 > 20

30 + 20 = 50 > 16

Observe o triângulo que foi formado com esses três segmentos na figura a seguir:

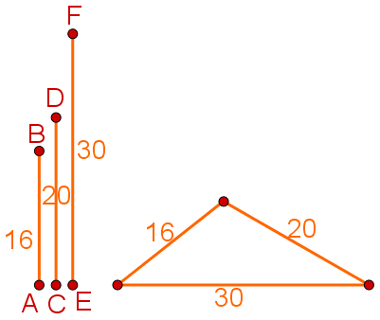
Se a soma entre os dois lados é igual ao terceiro, esse triângulonão pode existir. Além disso, as três desigualdades acima são conhecidas como desigualdade triangular.

Não é necessário fazer as três somas para verificar a possibilidade de um triângulo existir. Basta fazer a soma entre os dois lados menores. Se a soma entre eles for maior que o terceiro lado, então, a soma entre qualquer um deles e o terceiro lado (que é o maior) terá o mesmo resultado.

Exemplo: Um senhor deseja cercar um terreno triangular que possui e discute em uma loja que as dimensões do terreno são: 20 m x 15m x 5 m. Esse senhor mediu corretamente seu terreno?

A resposta é não. Como o terreno é triangular, se as medidas estivessem corretas, seria possível formar um triângulo. Entretanto, essas medidas não cumprem a desigualdade triangular:

20 + 15 = 35 > 5

20 + 5 = 30 > 15

15 + 5 = 20

Fundamentos da condição de existência

Suponha que uma pessoa queira demarcar uma parte de um terreno e possua apenas três varetas para isso. Ela resolve, então, que a marcação terá formato triangular e que os lados desse triângulo terão o mesmo comprimento das varetas. Sabendo que elas medem 2 metros, 3 metros e 4 metros, será possível construir esse triângulo?

A imagem a seguir foi feita para resolver esse problema e representa a fixação da vareta de 4 metros como base do triângulo. As extremidades das outras varetas foram presas às extremidades da base do triângulo e, em seguida, giradas as duas varetas a fim de que elas se encontrassem, como representado no esquema a seguir:

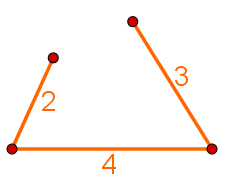
Para enxergar se as extremidades livres das varetas encontram-se de modo que o triângulo seja formado, observe a imagem abaixo, que contém a trajetória dessas extremidades.

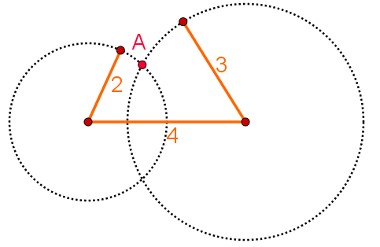
As extremidades das varetas encontram-se no ponto A.

Imagine também a mesma situação anterior, só que com varetas medindo 5 metros, 1 metro e 2 metros. A trajetória das varetas é igual à imagem a seguir:

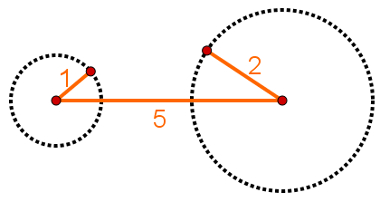
Na imagem acima, perceba que não existe possibilidade de fechar o triângulo com varetas que possuem essas medidas. Tendo em vista essas possibilidades, foi criada a noção de desigualdade triangular.

Por Luiz Paulo Moreira
Graduado em Matemática