O triângulo é um polígono formado por três lados. Isso quer dizer que é uma figura geométrica plana formada por três segmentos de reta que se encontram em suas extremidades, formando também três vértices e três ângulos internos. A área de um triângulo é a quantidade de plano que esse polígono ocupa no espaço onde é definido.
Dessa forma, a área é um número que está relacionado à quantidade do plano ocupada pela figura geométrica. Quando maior a área da figura, maior o espaço que ela ocupa e vice-versa.
Tópicos deste artigo
Fundamentos para o cálculo da área
O primeiro passo para determinar a área de uma figura geométrica qualquer é estabelecer uma unidade de medida de comprimento, que será usada para definir a unidade de medida de área.
Após isso, construa um quadrado que possua a medida do lado igual a 1 unidade da unidade de medida estabelecida. Por exemplo, determinando a unidade de medida como centímetro, esse quadrado deverá ter 1 centímetro de lado.
Esse quadrado será a unidade de medida base para a área de qualquer figura geométrica. Essa unidade de medida de área passa a ser chamada centímetro quadrado (cm2). Portanto, medir a área de uma figura em centímetros quadrados é o mesmo que determinar a quantidade de quadrados de lado igual a 1 cm que “cabem” no interior dessa figura, sem que haja espaços entre os quadrados ou que eles fiquem sobrepostos.
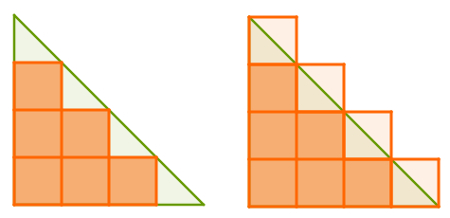
Na prática, não é necessário pensar nisso toda vez que for necessário calcular a área de alguma figura. Em algumas delas – especialmente em triângulos – sequer é possível preencher com quadrados sem que alguma parte do quadrado fique de fora da figura, ou de forma que toda a figura seja ocupada por quadrados de lado 1 un, como mostra a figura a seguir.
Nos dois casos mostrados acima, utilizando a técnica mencionada, não se pode afirmar que a área do triângulo verde é 9 e também não se pode afirmar que é 16. Para eliminar esse problema, existe uma fórmula para calcular a área do triângulo.
Área do triângulo
A fórmula que pode ser usada para calcular a área do triângulo é a seguinte:
A = bh
2
Nessa fórmula, b é a medida da base do triângulo e h é a medida de sua altura. Essa fórmula é obtida por meio de três passos:
O primeiro é determinar a área do retângulo. Note que contar a quantidade de quadrados usados para preencher um retângulo é o mesmo que multiplicar seu comprimento por sua largura, ou em outras palavras, sua base por sua altura.
O segundo é usar a área do retângulo e a decomposição de figuras geométricas para determinar a área do paralelogramo, que também é o produto de sua base por sua altura.
O terceiro é apenas perceber que todo triângulo é igual à metade de um paralelogramo, cortado por uma de suas diagonais.
Exemplos:
1- Determine a área de um triângulo cuja base mede 10 cm e a altura também mede 10 cm.
Solução:
A = bh
2
A = 10·10
2
A = 100
2
A = 50 cm2
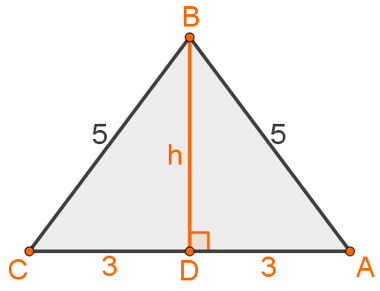
2- Qual a área de um triângulo que possui dois lados medindo 5 m e um lado medindo 6 m?
Solução:
Esse triângulo é isósceles. Considerando que sua base é o lado que mede 6 metros, construiremos a altura relativa a essa base. Exatamente porque o triângulo é isósceles, podemos garantir que essa altura também é a mediana da base dividindo-a em dois segmentos que medem 3 metros.
Assim, essa construção forma o triângulo ABD. Aplicando nele o teorema de Pitágoras, temos:
52 = h2 + 32
25 = h2 + 9
25 – 9 = h2
16 = h2
h = 4 m
Conhecendo a altura e a base do triângulo, podemos calcular sua área:
A = bh
2
A = 6·4
2
A = 24
2
A = 12 m2