O que são as dimensões do espaço?

A dimensão está relacionada à possibilidade de obter medidas em objetos definidos dentro de um espaço. É possível que alguns objetos não possam ser definidos em determinados espaços por causa do número de dimensões de que eles necessitam e do que é oferecido por esses espaços. Para que a construção de um objeto seja possível, é necessário que ele possua um número de dimensões igual ou inferior ao espaço.

Perceba que a palavra espaço não é usada apenas para o espaço tridimensional, mas para qualquer “lugar” que possua dimensões suficientes para a construção de objetos. Assim, as dimensões do espaço e os próprios espaços são os seguintes:

Espaço unidimensional e primeira dimensão

Quando dizemos que um espaço, ou objeto, possui apenas uma dimensão, estamos afirmando que somente é possível realizar um tipo de medida nesse espaço ou objeto. O espaço unidimensional é a reta.

Como as retas são conjuntos de pontos alinhados que não fazem curva, são infinitas e não apresentam espaços entre os pontos, então, não existe possibilidade de medir a largura delas. Assim, apenas é possível medir comprimentos de partes delas, chamadas segmentos de reta.

Dessa forma, a reta é o espaço que possui apenas uma dimensão. Os objetos que podem ser construídos nesse espaço são:

1 – Ponto;

2 – Segmentos de reta;

3 – Semirretas e

4 – Outras retas.

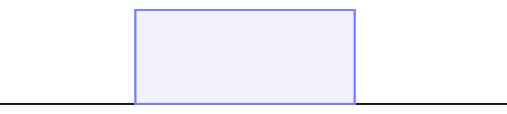
Suponha que seja necessário construir um retângulo. Essa figura geométrica possui largura e comprimento, que são duas medidas perpendiculares. Observe que, se colocarmos um dos lados do retângulo sobre o espaço unidimensional, todo o seu restante estará fora do espaço. Para construir essa figura geométrica, será necessário que exista outro espaço que contemple também a sua largura.

Retângulo sobre a reta

Espaço bidimensional e segunda dimensão

Quando o espaço é bidimensional, os objetos que podem ser definidos nele possuem até duas dimensões. Nesse tipo de espaço, é possível construir figuras que possuem comprimento e largura. O espaço bidimensional é o plano.

Algumas das figuras geométricas que podem ser definidas no plano são:

1 – Ponto;

2 – Retas, segmentos de reta e semirretas;

3 – Polígonos em geral;

4 – Círculos e circunferências.

Assim, o retângulo da imagem anterior pode ser definido no plano, que é o espaço bidimensional. A Geometria plana tem como base o espaço bidimensional, portanto, tudo o que é estudado nessa disciplina é construído sobre um plano.

Imagine agora um plano sobre o qual é colocada uma das bases de um prisma. A base do prisma pode ser definida no plano, mas o restante do sólido geométrico, não. Para que o prisma seja completamente construído, é necessário um espaço no qual exista a possibilidade de construção de objetos com profundidade.

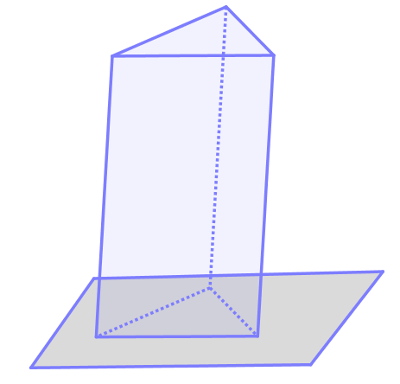
Prisma sobre o plano

Espaço tridimensional e terceira dimensão

O espaço tridimensional é composto pelo que conhecemos apenas como espaço. Esse espaço é infinito para todas as direções, e nele podem ser definidas todas as figuras e sólidos geométricos que são comumente estudados durante o Ensino Médio.

Dessa maneira, é possível definir no espaço tridimensional todas as figuras geométricas que possuem comprimento, largura e profundidade. Em outras palavras, todas as figuras que possuem três dimensões ou menos.

Quarta dimensão

Todo objeto que esteja incluído em um espaço tridimensional onde o tempo também conta como medida, na realidade, está em um espaço com quatro dimensões. O tempo é a medida responsável pela quarta dimensão.

É possível dizer ainda que as dimensões são infinitas (existem também a quinta, sexta, sétima etc.), mas não podem ser percebidas pelos sentidos humanos. Por isso, elas não são representadas geometricamente ou não ganham uma representação tão evidente quanto as outras.

Por Luiz Paulo Moreira
Graduado em Matemática