O que são monômios?

Afinal, o que são monômios? Os monômios são expressões algébricas que têm um número, conhecido como coeficiente, multiplicando uma ou mais letras (variáveis), a parte literal. Os monômios são a base para o estudo dos polinômios, podemos calcular adição, subtração, multiplicação e divisão entre os monômios. É possível saber o grau de um monômio, pois ele é determinado pela soma dos expoentes das suas variáveis. Todo polinômio é formado por monômios.

Leia também: O que são as expressões algébricas?

Tópicos deste artigo

• 1 - Resumo sobre monômios
• 2 - Como identificar um monômio?
• 3 - Grau de um monômio
• 4 - Monômios semelhantes
• 5 - Operações entre monômios
  • → Adição e subtração de monômios
  • → Multiplicação de monômios
  • → Divisão de monômios
  • → Potência de um monômio
• 6 - Diferenças entre monômios e polinômios
• 7 - Exercícios resolvidos sobre monômios

Resumo sobre monômios

• Monômio é uma expressão algébrica composta por um número (coeficiente) e uma ou mais variáveis elevadas a potências inteiras não negativas (parte literal).
• O grau de um monômio é determinado pela soma dos expoentes das suas variáveis.
• Dois monômios são classificados como monômios semelhantes quando eles têm a mesma parte literal.
• As operações com monômios incluem multiplicação, divisão, subtração e adição, sempre respeitando regras específicas.
• Para calcular tanto a adição quanto a subtração entre monômios, basta realizar a operação com o coeficiente e conservar a parte literal do monômio.
• Para calcular a multiplicação entre dois monômios, é necessário multiplicar tanto os seus coeficientes quanto a sua parte literal.
• Para dividirmos os monômios, basta dividirmos coeficiente com coeficiente e parte literal com parte literal.
• Para calcular a potência de um monômio, basta calcular a potenciação para o coeficiente e cada uma das variáveis.
• Monômios são a base para o estudo dos polinômios.

Como identificar um monômio?

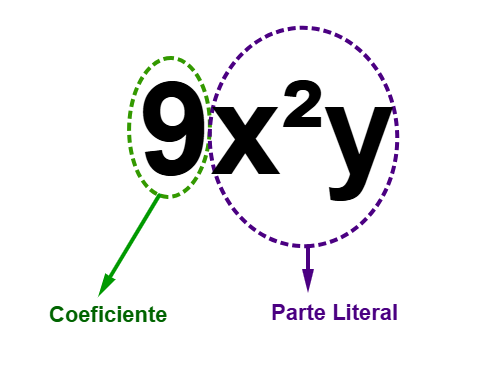
Os monômios são expressões algébricas que aparecem com frequência no estudo da álgebra. Para identificar um monômio, basta verificar se ele segue as características de uma expressão algébrica, que é ter um coeficiente, ou seja, um número multiplicando as variáveis; e ele tem apenas uma variável ou o produto de variáveis com expoentes inteiros não negativos.

• Exemplo de monômio:
  • 3a⁴
  • 5xt²y
  • $\frac{1}{2}x^6b$
  • 5x³
• Exemplo de não monômios:
  • 3x + 2y não é um monômio — note que temos uma soma entre dois termos algébricos, logo, esse exemplo não é um monômio.
  • $\frac{1}{x}$ não é um monômio — note que há variável no denominador, o que não pode acontecer em um monômio.

Grau de um monômio

O grau de um monômio é igual à soma dos expoentes de suas variáveis. Sendo assim, temos que:

• O monômio 4x²y tem grau 2 + 1 = 3.
• O monômio 5x⁴ tem grau 4.
• O monômio a²b³c tem grau 2 + 3 + 1 = 6.

Monômios semelhantes

Monômios semelhantes são dois monômios que tenham a mesma parte literal. É importante compreender que a parte literal deve ser idêntica, tanto nas variáveis quanto nos expoentes dessas variáveis. O conceito de monômios semelhantes é importante para aprendermos a realizar adição e subtração de monômios.

• Exemplos:
  • 9x² e 12x² são monômios semelhantes, pois ambos têm partes literais iguais a x².
  • 2xy²e5xy² são monômios semelhantes, pois ambos têm partes literais iguais a xy².
  • 3ab² e 2a²b não são monômios semelhantes, pois têm partes literais diferentes, ainda que as variáveis sejam as mesmas, ab² e a²b.
  • 3x e 3x³ não são monômios semelhantes, pois têm partes literais diferentes, x e x³.

Operações entre monômios

Conhecendo dois ou mais monômios, é possível realizar qualquer uma das quatro operações entre eles, ou seja, adição, subtração, multiplicação e divisão. Além dessas operações, é possível calcular a potência de um monômio.

→ Adição e subtração de monômios

Para que adição ou a subtração de monômios seja possível, é importante que esses monômios sejam monômios semelhantes, caso contrário, não podemos calcular a soma nem a diferença entre esses termos algébricos. Para calcular tanto a adição quanto a subtração entre monômios semelhantes, basta realizar a operação com o coeficiente e conservar a parte literal do monômio.

Exemplos:

• Calcule a soma:

4xy + 8xy

Note que esses monômios são semelhantes, pois têm a mesma parte literal. Para calcular a soma desses monômios, calcularemos a soma dos seus coeficientes:

4xy + 8xy = (4 + 8)xy = 12xy

• Calcule a diferença:

15ab² - 7ab²

A diferença é feita de forma análoga à da adição, então temos que:

15ab² - 7ab² = (15 - 7)ab² = 8ab²

• Calcule:

4x² + 9x² - 7x²

Agora faremos a conta de uma expressão que envolve tanto adição quanto subtração de monômios semelhantes. Utilizando o mesmo raciocínio, conservaremos a parte literal e realizaremos as operações entre os coeficientes.

4x² + 9x² - 7x² = (4 + 9 - 7)x² = (13 - 7)x² = 6x²

→ Multiplicação de monômios

A multiplicação entre monômios pode ser realizada independentemente de existir semelhança entre esses termos. Para calcular a multiplicação entre dois monômios, é necessário multiplicar tanto os seus coeficientes quanto a sua parte literal. Quando há variáveis que se repetem em ambos os termos, conservamos a base delas e somamos os seus expoentes, como a seguir:

Exemplos:

• Calcule:

$2x^2 \cdot 8x$

Calcularemos o produto entre os coeficientes, ou seja:

$2 \cdot 8 = 16$

Além disso, na parte literal, como são as mesmas variáveis, temos que:

$x^2\cdot x = x^3$

Então o produto será:

$2x^2\cdot 8x = 16x^3$

• Calcule:

$3ab^2\cdot 5a^2b^3c$

Multiplicando os coeficientes, temos que:

$3 \cdot 5 = 15$

Agora, na parte literal, é possível perceber que as variáveis a e b aparecem em ambos os termos:

$a\cdot a^2 = a^3$

$b^2\cdot b^3 = b^5$

Como a variável c aparece somente no segundo monômio, então ela vai aparecer na parte literal do produto, com os resultados encontrados; logo, temos que:

$3ab^2\cdot 5a^2b^3c = 15a^3b^5c$

• Calcule:

$4x^3y\cdot 3xy^3$

Utilizando o mesmo raciocínio dos exemplos anteriores, temos que:

$4 \cdot 3 = 12$

$x^3\cdot x = x^4$

$y\cdot y^3 = y^4$

Então o resultado será:

$4x^3y\cdot 3xy^3=12x^4y^4$

→ Divisão de monômios

Para dividirmos os monômios não é necessário que eles sejam semelhantes, basta dividirmos coeficiente com coeficiente e parte literal com parte literal. Quando há variáveis iguais na parte literal, calculamos a diferença entre os expoentes.

Exemplos:

• Calcule a divisão:

15x³ : 5x

Calculando a divisão entre os coeficientes, temos que:

15 : 5 = 3

Agora, entre a parte literal:

x³ : x = x^(3-1) = x²

Então encontramos como resultado:

15x³ : 5x = 3x²

• Calcule:

144x³y²z : 24xy²

Calcularemos a divisão encontre os coeficientes e a parte literal:

144 : 24 = 6

x³ : x = x² 

y² : y² = 1

Observações:

• Todo número dividido por ele mesmo tem resultado igual a 1, logo, y² : y² = 1.
• Note que a variável z só aparece no primeiro monômio, então a conservaremos na parte literal da divisão.

Após calcular a divisão entre esses monômios, o resultado será:

$144x^3y^2z : 24xy^2 = 6x^2 \cdot 1\cdot z=6x^2z$

• Calcule a divisão:

4a⁴b : 4a³b

Utilizando o mesmo raciocínio dos exemplos anteriores, temos que:

4 : 4 = 1

a⁴ : a³ = a

b : b = 1

Então, temos que:

4a⁴b : 4a³b = 1 ⋅ a ⋅ 1 = a

→ Potência de um monômio

Para calcular a potência de um monômio, basta calcular a potenciação para o coeficiente e cada uma das variáveis. Vale ressaltar que, para calcular potência de potência, conservamos a base e multiplicamos os expoentes. 

Exemplo:

• Calcule:

(3x³y⁴)²

Calculando a potência, temos que:

3² = 9

$(x^3)^2 = x^{(3\cdot 2)} = x^6$

$(y^4)^2 = y^{(4\cdot 2)} = y^8$

Então temos que:

(3x³y⁴)² = 9x⁶y⁸

• Calcule:

(2a³b⁴c)³

Então temos que:

2³ = 8

$(a^3)^3 = a^{(3\cdot 3)}=a^9$

$(b^4)^3 = b^{(4\cdot 3)}=b^{12}$

$(y^8)^3 = y^{(8\cdot 3)}=y^{24}$

Assim, a potência do monômio será:

(2a³b⁴c)³ = 8a⁹b¹²y²⁴

Diferenças entre monômios e polinômios

O estudo dos monômios é base para o estudo dos polinômios. Na álgebra, um dos conceitos mais importantes é o de polinômio, que nos permite estudar variáveis e funções posteriormente. A diferença entre polinômios e monômios é que os polinômios podem ter mais de um termo algébrico, podendo haver soma ou subtração de monômios em sua formação. Veja os exemplos:

• Exemplos de monômio:

3x²

2y

• Exemplos de polinômio:

3x² + 2y

4x³ - 3y

Para saber mais detalhes sobre os polinômios, clique aqui.

Exercícios resolvidos sobre monômios

Questão 1

Qual das seguintes expressões é um monômio?
A) 3x + 5
B) 2y³
C) 4x² − 7
D) x² + 2y
E) $\frac{2}{x}$

Resolução:

Alternativa B

Analisando as alternativas, podemos verificar que, nas alternativas A, C e D, temos mais de um termo, ou seja, há uma adição entre os termos algébricos, e, para ser monômio, é necessário que exista um único termo. Sendo assim, a alternativa que corresponde a um monômio é a B. Para eliminar a alternativa E, basta verificar que a variável está no denominador, então essa expressão algébrica não corresponde a um monômio.

Questão 2

Simplifique (2x³) (4x²) e responda qual é o grau do monômio encontrado após calcular esse produto:

A) 2

B) 3

C) 5

D) 6

E) 9

Resolução:

Alternativa C

Primeiro calcularemos o produto:

$2x^3\cdot 4x^2$

$2 \cdot 4 = 8$

$x^3\cdot x^2 = x^{(3 + 2)} = x^5$

Então o produto é igual a:

$2x^3\cdot 4x^2=8x^5$

Para calcular o grau desse polinômio, basta analisar o expoente da parte literal, que, no caso, é 5, então o grau desse monômio é 5.

Fontes

Giovanni, J., Castrucci, B., & Machado, J. R. (Ano). Matemática: Contexto e Aplicações. 2ª ed. São Paulo: FTD

Iezzi, G., & Murakami, C. (Ano). Fundamentos de Matemática Elementar: Vol. Único. 9ª ed. São Paulo: Atual Editora