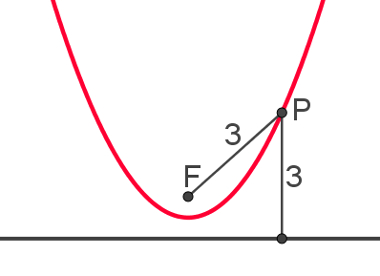
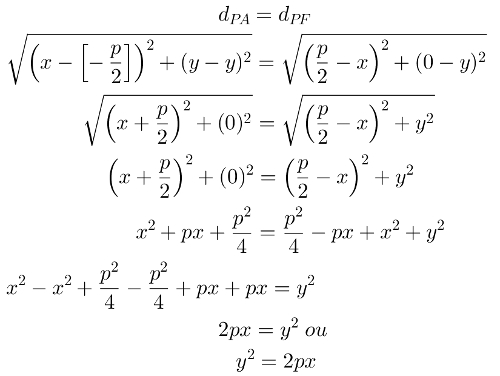Considerando-se um ponto F e uma reta r no plano, o conjunto que contém todos os pontos cuja distância até F é igual à distância até r é chamado parábola. O ponto F é o foco da parábola e jamais poderá ser um dos pontos da reta r. Caso contrário, a distância entre F e r sempre será igual a zero.
A seguir, um exemplo de parábola com a demonstração de seu ponto F e a reta r.
No ensino fundamental, as parábolas são usadas apenas para representar geometricamente funções do segundo grau. No ensino médio, elas também são resultado de estudos das cônicas, em Geometria Analítica.
Elementos de uma parábola
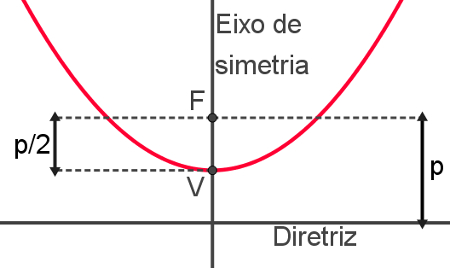
São cinco os principais elementos da parábola. Eles são figuras geométricas que recebem nomes especiais devido à sua função e à sua importância na definição das parábolas. São eles:
a) Foco
É o ponto F usado para a definição da parábola.
b) Diretriz
É a reta r, também usada na definição da parábola. Lembre-se de que a distância entre um ponto qualquer da parábola e a reta r tem a mesma distância que esse mesmo ponto e o seu foco.
c) Parâmetro
O parâmetro de uma parábola é a distância entre o seu foco e sua diretriz. Essa distância é o comprimento do segmento de reta que liga o foco e a diretriz, formando com ela um ângulo reto. Para encontrar esse valor, pode-se usar a distância entre ponto e reta.
d) Vértice é o ponto da parábola que fica mais próximo de sua diretriz. Uma das propriedades desse ponto é que a sua distância até o foco da parábola é igual à metade do parâmetro. Também podemos dizer que a distância entre esse ponto e a diretriz da parábola é igual à metade do parâmetro.
Seja a medida do parâmetro de uma parábola representada pela letra p, a medida do segmento VF será dada por:
VF = P
2
e) Eixo de simetria
O eixo de simetria de uma parábola é uma reta perpendicular à diretriz que passa pelo seu vértice. Consequentemente, essa reta também passa pelo foco da parábola e contém o segmento chamado parâmetro.
A imagem a seguir mostra cada um dos elementos de uma parábola:
Equações reduzidas da parábola
Existem duas equações reduzidas da parábola:
y2 = 2px
e
x2 = 2py
Essas equações são obtidas colocando o vértice de uma parábola na origem de um plano cartesiano. Primeiramente, suponha que a diretriz dessa parábola é paralela ao eixo y do plano, como mostra imagem a seguir.
Escolhendo um ponto P(x, y) qualquer na parábola, teremos as seguintes hipóteses:
1 – Coordenadas de F: como o segmento VF = p/2, então as coordenadas de F são (p/2, 0). Para perceber isso, note que o eixo x, nessa construção, é o eixo de simetria da parábola.
2 – Coordenadas de A: o ponto A pertence à diretriz, e a distância de P até A é igual à distância de P até F. Assim, mudando a posição do ponto P, sempre teremos essa característica. As coordenadas de A são: (– p/2, y).
Isso acontece porque A sempre estará à mesma altura de P, e sua distância até o eixo y é a mesma que a distância de V até F, com sinal invertido.
3 – A distância de P até A é igual à distância de P até F, pois essa é a definição da parábola.
Diante dessas hipóteses, podemos calcular a seguinte equação, substituindo nela as coordenadas de cada um dos pontos P, A e F:
A segunda equação da parábola tem seus cálculos e construções feitos de maneira análoga a esses, entretanto, apresenta a diretriz paralela ao eixo x.
Por Luiz Paulo Moreira
Graduado em Matemática