Pirâmides são poliedros construídos a partir de uma base poligonal e um ponto fora do plano onde se encontra essa base. São tridimensionais e, por isso, elas só podem ser definidas em um espaço que possui três ou mais dimensões. A definição formal das pirâmides é a seguinte:
Uma pirâmide é o conjunto de segmentos de reta cujas extremidades são um polígono e um ponto fora do plano que contém esse polígono. Veja:
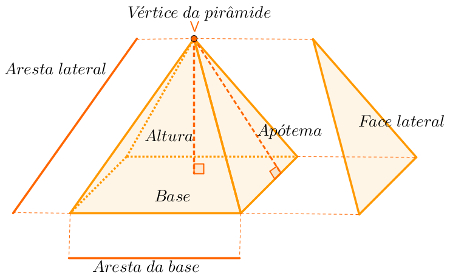
Elementos de uma pirâmide
Como as pirâmides são sólidos geométricos formados basicamente por segmentos de reta, podemos encontrar nelas alguns elementos, a saber:
-
Faces: são os polígonos que podem ser observados nesse poliedro;
-
Arestas: são os segmentos de reta formados nas intersecções das faces;
-
Vértices: são os pontos de encontro entre as arestas;
-
Vértice da pirâmide: é o ponto V na figura acima;
Anuncie aqui -
Base: polígono usado na definição da pirâmide;
-
Arestas da base: arestas que pertencem à base;
-
Arestas laterais: arestas que não pertencem à base da pirâmide;
-
Faces laterais: faces da pirâmide que não são a sua base;
-
Altura da pirâmide: distância entre o vértice da pirâmide e o plano que contém sua base;
-
Secção transversal: intersecção da pirâmide com um plano paralelo à base;
Anuncie aqui -
Apótema: altura de uma face lateral com relação à base de uma pirâmide regular.
Classificação de uma pirâmide
As pirâmides podem ser classificadas de acordo com o seu número de faces. Note que esse número sempre é igual ao número de lados da base somado a uma unidade. Note também que, exceto pela base da pirâmide, todas as faces são triangulares.
-
Pirâmide triangular: possui um triângulo como base;
-
Pirâmide quadrangular: possui um quadrilátero como base;
-
Pirâmide pentagonal: possui um pentágono como base.
Anuncie aqui
E assim segue a classificação, que depende do número de arestas da base da pirâmide. Vale ressaltar que a pirâmide triangular também é chamada de tetraedro.
Pirâmide regular
Um poliedro é regular quando é um poliedro de Platão e, simultaneamente, suas faces são polígonos congruentes e regulares.
No caso específico da pirâmide, a regularidade também pode ser verificada da seguinte maneira: se a base é um polígono regular e o segmento de reta que representa a altura possui o centro da base como segunda extremidade, a pirâmide é regular.
A propriedade das pirâmides regulares é a seguinte: arestas laterais são congruentes e faces laterais são triângulos isósceles.
Por Luiz Paulo Moreira
Graduado em Matemática

