Multiplicidade de uma raiz

Na resolução da equação do 2º grau x² – 6x + 9 = 0, encontramos duas raízes iguais a 3. Utilizando o teorema da decomposição, fatoramos o polinômio e obtemos:
x² – 6x + 9 = 0 = (x – 3)(x – 3) = (x – 3)²

Nesse caso, dizemos que 3 é raiz de multiplicidade 2 ou raiz dupla da equação.
Dessa forma, se um polinômio fatorado resulta a seguinte expressão:

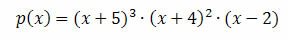
Podemos dizer que:
x = -5 é raiz com multiplicidade 3 ou raiz tripla da equação p(x) = 0
x = -4 é raiz com multiplicidade 2 ou raiz dupla da equação p(x) = 0
x = 2 é raiz com multiplicidade 1 ou raiz simples da equação p(x) = 0
De maneira geral, dizemos que r é uma raiz de multiplicidade n, com n ≥ 1, da equação p(x) = 0, se:

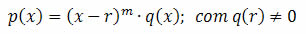
Observe que p(x) é divisível por (x – r)^m e que a condição q(r) ≠ 0 significa que r não é raiz de q(x) e garante que a multiplicidade da raiz r não é maior que m.

Exemplo 1. Resolva a equação x⁴ – 9x³ + 23x² – 3x – 36 = 0, sabendo que 3 é raiz dupla.
Solução: considere p(x) como sendo o polinômio dado. Assim:


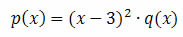
Note que q(x) é obtido fazendo a divisão de p(x) por (x – 3)².
Fazendo a divisão pelo dispositivo prático de Briot –Ruffini, obtemos:

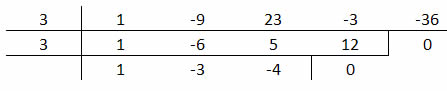
Após a realização da divisão, vemos que os coeficientes do polinômio q(x) são 1, -3 e -4. Assim, q(x) = 0 será: x² – 3x – 4 = 0
Vamos resolver a equação acima para determinarmos as demais raízes.
x² – 3x – 4 = 0
Δ = (-3)2 - 4*1*(-4)
Δ = 25
x = -1 ou x = 4
Portanto, S = {-1, 3, 4}

Exemplo 2. Escreva uma equação algébrica de grau mínimo tal que 2 seja raiz dupla e – 1, raiz simples.
Solução: Temos que:
(x – 2)(x – 2 )(x – (-1)) = 0
Ou

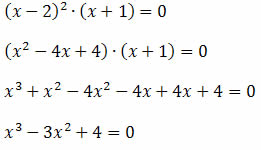
Por Marcelo Rigonatto
Especialista em Estatística e Modelagem Matemática
Equipe Brasil Escola

Polinômios - Matemática - Brasil Escola