Inequação do 2º grau é uma expressão algébrica com desigualdade em que o maior expoente da incógnita é 2. Resolver uma inequação significa determinar qual intervalo de valores que a incógnita pode assumir para satisfazer a expressão. Outra forma de resolver uma inequação do 2° grau é analisar o gráfico da função do 2° grau associada.
Leia também: Inequação modular — expressão algébrica com desigualdade que possui uma variável dentro do módulo
Tópicos deste artigo
- 1 - Resumo sobre inequação do 2º grau
- 2 - O que é uma inequação do 2º grau?
- 3 - Como resolver uma inequação do 2º grau?
- 4 - Exercícios resolvidos sobre inequações do 2º grau
Resumo sobre inequação do 2º grau
- Inequação do 2º grau é uma expressão com desigualdade em que o maior expoente da incógnita é 2.
- Para resolvê-la, devemos obter as raízes da equação associada e analisar os sinais da incógnita para valores em cada intervalo determinado pelas raízes.
- Outra forma de encontrar a solução dela é analisar o gráfico da função associada.
O que é uma inequação do 2º grau?
Uma inequação do 2º grau é uma expressão algébrica com desigualdade em que o maior expoente da incógnita é 2. Assim, a inequação do 2º grau apresenta um dos seguintes formatos, em que a, b e c são números reais:
- \( ax^2+bx+c<0\)
- \( ax^2+bx+c\le0\)
- \( ax^2+bx+c>0\)
- \( ax^2+bx+c\geq0\)
Lembre-se de que os sinais <, ≤,>,≥ indicam desigualdades e significam, respectivamente, “menor”, “menor ou igual”, “maior” e “maior ou igual”.
Exemplo:
\(x^2-4<0\) é uma inequação do 2º grau, com a=1, b=0 e c=-4. Resolva essa inequação.
Resolução:
Resolver essa inequação é indicar quais números reais podemos substituir a incógnita x para que \(x^2-4<0\). Vamos testar alguns números.
- Se \(x=-3\), temos que \(\left(-3\right)^2-4\ =9-4=5\). Como 5 não é menor que 0, o número –3 não é uma solução para a inequação.
- Se \(x=0\), temos que \(0^2-4=-4\). Como – 4 é menor que 0, o número 0 é uma solução para a inequação.
- Se \(x=5\), temos que \(1^2-4=1-4=-3\). Como –3 é menor que 0, o número 1 é uma solução para a inequação.
- Se \(x=5,5\), temos que \(\left(5,5\right)^2-4=30,25-4=26,25\). Como 26,25 não é menor que 0, o número 5,5 não é uma solução para a inequação.
Encontramos duas soluções para a inequação, e poderíamos continuar testando números para encontrar outras. No entanto, resolver a inequação significa encontrar todas as soluções, ou seja, determinar o intervalo do conjunto solução. Vejamos, a seguir, como fazer isso.
Como resolver uma inequação do 2º grau?
Para resolver uma inequação do 2º grau, devemos seguir os seguintes passos:
- 1º passo: comparar a expressão com a equação do 2º grau correspondente.
- 2º passo: obter as raízes da equação.
- 3º passo: atribuir valores para a incógnita com base nos intervalos de números reais determinados pelas raízes da equação e avaliar quais satisfazem a inequação.
Exemplo:
Determine o conjunto solução da inequação do 2º grau \(x^2-4<0\).
Resolução:
Vamos analisar a equação do 2º grau correspondente:
\(x^2-4=0\)
\(x^2=4\)
Assim, \(x_1=-2 \ e\ x_2=2\) são as raízes da equação \(x^2-4=0\).
Agora vamos analisar o que ocorre na expressão \(x^2-4\) para os números reais nos intervalos definidos por –2 e 2. Lembre-se de que buscamos valores de x, em que \(x^2-4<0\).
- Se \(x<-2\), tem-se que \(x^2-4\) é maior que zero.
(Testamos \(x=-3\) anteriormente e obtemos 5 como resultado. Poderíamos atribuir outros valores para x com \(x<-2\) e teríamos que \(x^2-4 \) é maior que zero.)
- Se \(-2 < x < 2\), tem-se que \(x^2-4\) é menor que zero.
(Testamos \(x = 0\) e \(x = 1\) anteriormente e obtemos –4 e –3, respectivamente, como resultados. Poderíamos atribuir outros valores para x, com \(-2 < x < 2\), e teríamos que \(x^2-4 \) é menor que zero.)
- Se \(2 < x\), tem-se que \(x^2-4\) é maior que zero.
(Testamos \(x=5,5\) anteriormente e obtemos 26,25 como resultado. Poderíamos atribuir outros valores para x, com \(2 < x\), e teríamos que \(x^2-4\) é maior que zero.)
Dessa forma, o conjunto solução é \(S = \{ x \in R / -2 < x < 2 \}\)
→ Outra forma de resolver uma inequação do 2º grau
Um modo mais direto de resolver uma inequação do 2° grau é analisar os sinais do gráfico da função do 2º grau à qual a inequação do 2º grau está associada. Considerando uma função do 2° grau \(f\left(x\right)=ax^2+bx+c\), o gráfico desse tipo de função é uma parábola cuja concavidade está associada ao sinal de a:
- Se a>0, a concavidade é voltada para cima.
- Se a<0, a concavidade é voltada para baixo.
Exemplo:
Qual o conjunto solução da inequação \(2x^2-6x+4\geq0\)?
Resolução:
Vamos analisar a equação do 2º grau correspondente:
\(2x^2-6x+4=0\)
Utilizando a fórmula de Bháskara, temos que:
\(x=\frac{6\pm\sqrt{36-4\cdot2\cdot4}}{4}\)
Assim, \(x_1=1 \ e\ x_2=2 \) são as raízes da equação \(2x^2-6x+4=0\).
Agora considere a função \(f\left(x\right)=2x^2-6x+4\). Como 2>0, o gráfico dessa função é uma parábola com concavidade para cima. Além disso, pelo que analisamos, o gráfico dessa função cruza o eixo horizontal quando x=1 e quando x=2. Assim, o comportamento dessa função próximo a esses valores é o seguinte:
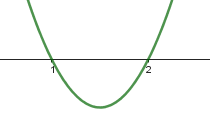
Note que:
- Se x<1, tem-se que \(2x^2-6x+4\) é maior que zero.
- Se 1< x < 2, tem-se que \(2x^2-6x+4\) é menor que zero.
- Se 2 < x, tem-se que \(2x^2-6x+4\) é maior que zero
Portanto, o conjunto solução da inequação \(2x^2-6x+4\geq0 \ é \ S=\{x\in R/x\le1\ \mathrm{ou\ }2\le x\}\).
Veja também: Sistema de inequação do 1º grau — formado por duas ou mais inequações do 1º grau
Exercícios resolvidos sobre inequações do 2º grau
Questão 1
(Udesc) O conjunto solução da inequação \(x^2-2x-3\le0\) é:
A) \( \{x\in R/-1\ < x < 3\}\)
B) \( \{x\in R/-1\ < x \leq 3\}\)
C) \( \{x\in R/x<-1\ \mathrm{ou\ }x>3\}\)
D) \( \{x\in R/x<-1\ \mathrm{ou\ }x\geq3\}\)
E) \( \{x\in R/-1\le x\le3\}\)
Resolução:
Alternativa E
Considere a equação \(x^2-2x-3=0\). Utilizando a fórmula de Bháskara, temos que:
\(x=\frac{2\pm\sqrt{4-4\cdot1\cdot-3}}{2}\)
Assim, \(x_1=-1 \ e\ x_2=3\) são as raízes da equação \(x^2-2x-3=0\).
Considere \(f\left(x\right)=x^2-2x-3\). O gráfico dessa função possui a concavidade para cima e cruza o eixo horizontal em \(x_1=-1 \ e\ x_2=3\).
Portanto, os valores de x, em que \(x^2-2x-3\le0\), são os valores de –1 a 3, incluido \(x=-1 \ e\ x=3\).
Questão 2
(PUC) Quantas soluções inteiras a inequação \(x^2+x-20\le0\) admite?
A) 2
B) 3
C) 7
D) 10
E) 13
Resolução:
Alternativa D
Considere a equação \(x^2+x-20=0\). Utilizando a fórmula de Bháskara, temos que:
\(x=\frac{-1\pm\sqrt{1-4\cdot1\cdot-20}}{2}\)
Assim, \(x_1=-5 \ e\ x_2=4\) são as raízes da equação \(x^2+x-20=0\).
Considere \(f\left(x\right)=x^2+x-20\). O gráfico dessa função possui a concavidade para cima e cruza o eixo horizontal em x1=-5 e x2=4.
Portanto, os valores de x, em que \(x^2+x-20\le0\), são os valores de – 5 a 4, incluido \(x=-5 \ e\ x=4\). Dessa forma, o conjunto com as soluções inteiras é:
\(\{-5,\ -4,-3,-2,-1,\ 0,\ 1,\ 2,\ 3,\ 4\}\)
Fontes
LIMA, Elon L. et al. A Matemática do Ensino Médio: Volume 1. Coleção Professor de Matemática. Rio de Janeiro: SBM, 2016.
MINEIRO, R. M. Estudo das três dimensões do problema didático de inequações. Tese (Doutorado em Educação Matemática) - Programa de Estudos Pós-Graduados em Educação Matemática, Pontifícia Universidade Católica de São Paulo, São Paulo, 2019. Disponível em https://repositorio.pucsp.br/jspui/handle/handle/22984.

