A equação é caracterizada pelo sinal da igualdade (=). A inequação é caracterizada pelos sinais de maior (>), menor (<), maior ou igual (≥) e menor ou igual (≤).
• Dada a função f(x) = 2x – 1 → função do 1º grau.
Se dissermos que f(x) = 3, escreveremos assim:
2x – 1 = 3 → equação do 1º grau, calculando o valor de x, temos:
2x = 3 + 1
2x = 4
x = 4 : 2
x = 2 → x deverá valer 2 para que a igualdade seja verdadeira.
• Dada a função f(x) = 2x – 1. Se dissermos que f(x) > 3, escrevemos assim:
2x – 1 > 3 → inequação do 1º grau, calculando o valor de x, temos:
2x > 3 + 1
2x > 4
x > 4 : 2
x > 2 → esse resultado diz que para que essa inequação seja verdadeira o x deverá ser maior que 2, ou seja, poderá assumir qualquer valor, desde que seja maior que 2.
Assim, a solução será: S = {x ![]() R | x > 2}
R | x > 2}
• Dada a função f(x) = 2(x – 1). Se dissermos que f(x) ≥ 4x -1 escreveremos assim:
2(x – 1) ≥ 4x -1
2x – 2 ≥ 4x – 1 → unindo os termos semelhantes temos:
2x – 4x ≥ - 1 + 2
- 2x ≥ 1 → multiplicando a inequação por -1, temos que inverter o sinal, veja:
2x ≤ -1
x ≤ - 1 : 2
x ≤ -1→ x assumirá qualquer valor, desde que
2 seja igual ou menor que 1.
Assim, a solução será: S = { x ![]() R | x ≤ -1}
R | x ≤ -1}
2
Podemos resolver as inequações de outra forma, utilizando gráficos, veja:
Vamos utilizar a mesma inequação do exemplo anterior 2(x – 1) ≥ 4x -1, resolvendo ficará assim:
2(x – 1) ≥ 4x -1
2x – 2 ≥ 4x – 1
2x – 4x ≥ - 1 + 2
-2x – 1 ≥ 0 → chamamos -2x – 1 de f(x).
f(x) = - 2x – 1, achamos o zero da função, para isso basta dizer que f(x) = 0.
-2x – 1 = 0
-2x = 0 + 1
-2x = 1 (-1)
2x = -1
x = -1
2
Assim, a solução da função será: S = { x ![]() R | x = -1 }
R | x = -1 }
2
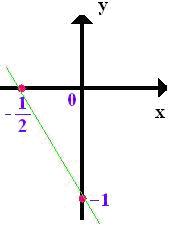
Para construirmos o gráfico da função f(x) = - 2x – 1 basta saber que nessa função
a = -2 e b = -1 e x = -1, o valor de b é onde a reta passa no eixo y e o valor de x é
2
onde a reta corta o eixo x, assim, temos o seguinte gráfico:
Então, observamos a inequação -2x – 1 ≥ 0, quando passamos pra função achamos que
x ≤ – 1 , então chegamos a solução seguinte:
2
S = { x ![]() R | x ≤ -1 }
R | x ≤ -1 }
2
Por Danielle de Miranda
Equipe Brasil Escola