Inequações logarítmicas

As inequações logarítmicas são todas aquelas que apresentam logaritmos. A incógnita, nesses casos, está no logaritmando e/ou na base. Vale lembrar que um logaritmo possui o seguinte formato:

log_a b = x ↔ a^x = b,

*a é a base do logaritmo; b é o logaritmando e x é o logaritmo.

Para resolver inequações logarítmicas, aplicamos as propriedades operatórias dos logaritmos e os conceitos tradicionais de resolução de inequações. Assim como fazemos com as equações logarítmicas, é importante verificar as condições de existência dos logaritmos (tanto a base quanto o logaritmando devem ser maiores que zero).

Ao desenvolver as inequações logarítmicas, podemos alcançar duas situações:

1º) Desigualdade entre logaritmos de mesma base:

log_a b < log_a c

Temos aqui dois casos a serem analisados: se a base for maior do que 1 (a > 1), podemos desconsiderar o logaritmo e manter a desigualdade entre os logaritmandos, isto é:

Se a > 1, então log_a b < log_a c ↔ b < c

Se, em contrapartida, a base for um número entre 0 e 1 (0 > a > 1), ao resolver a inequação logarítmica, devemos inverter a desigualdade e estabelecer uma inequação entre os logaritmandos, ou seja:

Se 0 > a > 1, então log_a b < log_a c ↔ b > c

2º) Desigualdade entre um logaritmo e um número real:

log_a b < x

Se, ao resolver uma inequação logarítmica, depararmo-nos com uma desigualdade entre um logaritmo e um número real, podemos aplicar a propriedade básica do logaritmo, mantendo intacto o símbolo da desigualdade:

log_a b < x ↔ b < a^x

ou

log_a b > x ↔ b > a^x

Vejamos alguns exemplos de resolução de inequações logarítmicas:

Exemplo 1: log₅ (2x – 3) < log₅ x

Devemos verificar as condições de existência dos logaritmos:

Temos uma desigualdade entre logaritmos de mesma base que é maior do que 1. Podemos então manter a desigualdade apenas entre os logaritmandos:

log₅ (2x – 3) < log₅ x
2x – 3 < x
2x – x < 3
x < 3

Quadro de resolução do Exemplo 1

Nesse caso, a solução é

.

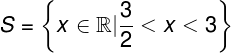
Exemplo 2: log₂ (x + 3) ≥ 3

Primeiramente, verificamos a condição de existência do logaritmo:

x + 3 > 0
x > – 3

Nesse caso, há uma desigualdade entre um logaritmo e um número real. Podemos resolver o logaritmo da forma convencional, mantendo a desigualdade:

log₂ (x + 3) ≥ 3
x + 3 ≥ 2³ 
x + 3 ≥ 8
x ≥ 8 – 3
x ≥ 5 
 

Quadro de resolução do Exemplo 2

A solução é .

Exemplo 3: log_1/2 3x > log_1/2 (2x + 5)

Verificando as condições de existência dos logaritmos, temos:

Nesse exemplo, há uma desigualdade entre logaritmos de mesma base que é menor do que1. Para resolvê-la, devemos inverter a desigualdade, aplicando-a entre os logaritmandos:

log_1/2 3x > log_1/2 (2x + 5)
3x < 2x + 5
3x – 2x < 5
x < 5

Quadro de resolução do Exemplo 3

Nesse caso, a solução é ​.

Por Amanda Gonçalves
Graduada em Matemática