Elipse

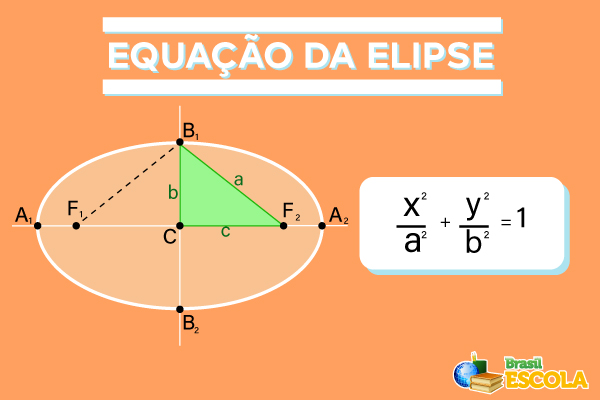
A elipse é uma figura plana classificada como uma cônica, pois ela pode ser obtida da secção de um plano em um cone. Encontrar uma figura plana com forma de elipse é bastante comum no dia a dia. Ela foi amplamente estudada para explicar a movimentação dos planetas ao redor do Sol, pois as órbitas desses astros são elipses.

A geometria analítica é a área da matemática que busca descrever de forma algébrica as formas geométricas, inclusive, a elipse é estudada a fundo na geometria analítica, sendo possível descrevê-la por meio de uma equação que leva em consideração seus elementos. Os principais elementos da elipse são:

• eixo maior

• eixo menor

• distância focal

• focos F₁ e F₂

Definimos a elipse como o conjunto de pontos em que a soma da distância desses pontos ao foco F₁ e ao foco F₂ é sempre constante.

Leia também: Quais são as diferenças entre figuras planas e espaciais?

Tópicos deste artigo

• 1 - O que é elipse?
• 2 - Elementos da elipse
• 3 - Equação da elipse
• 4 - Excentricidade da elipse
• 5 - Área da elipse
• 6 - Exercícios resolvidos

O que é elipse?

Conhecemos como elipse a figura plana formada pela secção entre o plano e o cone, da seguinte maneira:

Para construir a elipse, é necessário conhecer seus dois focos, F₁ e F₂, e também o comprimento do eixo maior, que é o seguimento de reta que liga as extremidades da elipse, na imagem a seguir, representado por A₁ A₂.

O comprimento do eixo maior é igual a 2a, então, a elipse é a curva formada por todos os pontos P_n em que a soma da distância do ponto até o primeiro foco (dP_nF₁) com a distância do ponto até o segundo foco (dP_nF₂) é sempre constante e igual a 2a.

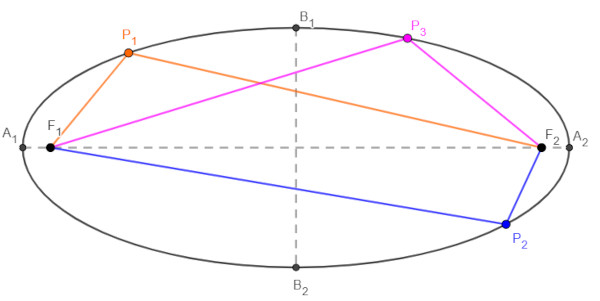
dP₁F₁ + dP₁F₂ = dP₂F₁ + P₂F₂ = dP₃F₁ + dP₃F₂ = dA₁A₂ = 2a

Elementos da elipse

Para compreender bem a formação da elipse, é necessário conhecer cada um de seus elementos. São eles os focos, o centro, o eixo maior e o eixo menor. Com base neles, é possível traçar relações importantes na elipse.

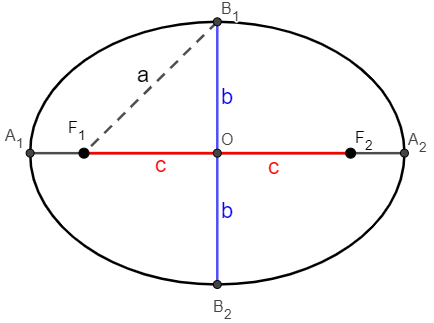
• O centro da elipse é representado pelo ponto O.

• Já os pontos F₁ e F₂ representam os focos de elipse.

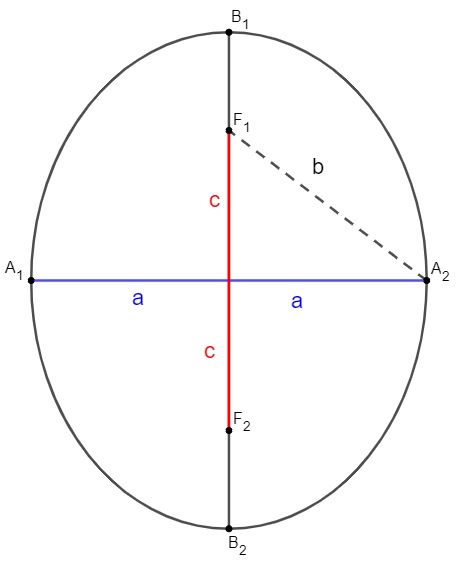
• Os pontos A₁ e A₂ são extremidades do eixo horizontal da elipse, e os pontos B₁ e B₂ são extremidades do seu eixo vertical.

• A distância entre B₁ e B₂ é igual a 2b (comprimento da elipse no eixo menor).

• A distância entre A₁ e A₂ é igual a 2a (comprimento da elipse no eixo maior).

• A distância focal entre F₁ e F₂ é igual a 2c.

Observação: É importante perceber que o seguimento F₁B₁ tem comprimento igual à metade do eixo horizontal, ou seja, dF₁B₁ = a. Sendo assim, é possível perceber também uma importante relação pitagórica ao analisar o triângulo A₁OB_1. Note que ele é um triângulo retângulo. Sendo assim, podemos aplicar o teorema de Pitágoras.

a² = b² + c²

Existe outra possibilidade para a elipse, que é quando o maior eixo é o eixo vertical. Nesse caso, os elementos continuam os mesmos.

Nesse caso podemos aplicar o teorema de Pitágoras também, ficando da seguinte maneira:

b² = a² + c²

Leia também: Quais são os elementos de um polígono?

Equação da elipse

O estudo da elipse de forma analítica é feito no plano cartesiano. A geometria analítica busca descrever, por meio de equações, as figuras da geometria plana. Sendo assim, é possível descrever a figura por meio da chamada equação da elipse.

Primeiro faremos exemplos de uma elipse cujos focos estão contidos ou no eixo x ou no eixo y, ou seja, a origem da elipse coincide com a origem do plano cartesiano.

Nesse caso existem duas possibilidades, quando o eixo maior é o eixo vertical e quando o eixo maior é o eixo horizontal:

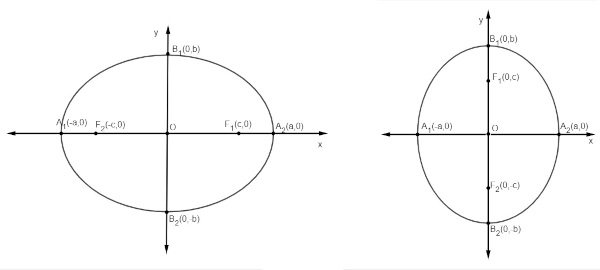
Observação: Os focos sempre estão contidos no maior eixo, então, se a > b, os focos estão contidos no eixo horizontal, e se b > a, eles estão contidos no eixo vertical.

Nem sempre o centro da elipse está na origem do plano cartesiano, o que não impede o desenvolvimento e a adaptação da equação da elipse para esse caso. Quando a elipse está deslocada da origem O( x_0, y₀), sua equação pode ser descrita por:

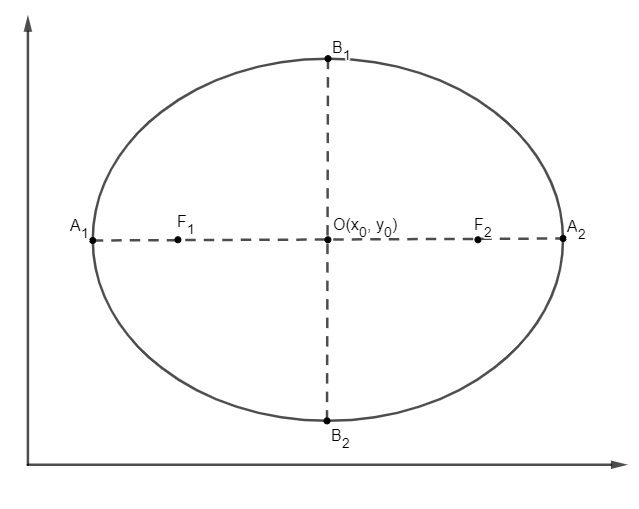
Leia também: Qual é a equação reduzida da circunferência?

Excentricidade da elipse

Conhecemos como excentricidade a razão entre o comprimento c e a metade do comprimento do maior eixo da elipse. Supondo que o maior eixo é o horizontal, a excentricidade é calculada por:

Caso a elipse estiver no eixo vertical, a excentricidade será calculada por:

A excentricidade nos diz o quão achatada é a elipse, quanto maior for o valor da excentricidade, mais próximo de uma circunferência estará a elipse. Como o eixo maior tem sempre comprimento maior que a distância focal, então, consequentemente, c < a, logo, essa divisão é sempre um número entre 0 e 1.

Área da elipse

Como a elipse tem um formato arredondado, para calcular a sua área, utilizamos a constante π e também a medida da metade do comprimento horizontal e a da metade do comprimento vertical, então, temos que:

A = abπ

A: comprimento da elipse
a: metade do comprimento do eixo horizontal
b: metade do comprimento do eixo vertical

Exemplo:

Calcule a área de uma elipse, com os focos no eixo horizontal, cujo eixo maior mede 50 cm, e o menor, 36 cm.

Como o eixo maior é o horizontal, então, os focos estão contidos nele. Sendo assim, temos que:

2a = 50

a = 50/2

a = 25

E no eixo vertical, temos que:

2b = 36

b = 36/2

b = 18

Então a área da elipse é dada por:

A = abπ

A = 25 · 18π

A = 450π cm²

Exercícios resolvidos

Questão – (IFB) Considerando uma elipse com centro na origem, focos num dos eixos coordenados e passando pelos pontos (5, 0) e (0, 13), determine os focos da elipse.

a) (13, 0) e (-13, 0)
b) (0, 13) e (0, -13)
c) (12, 0) e (-12, 0)
d) (0, 12) e (0, -12)
e) (5, 0) e (-5, 0)

Resolução

Alternativa D

Note que ela passa no ponto (0, 13), o que indica que b = 13, e também que ela passa pelo ponto (5,0) a = 5. Como b > a, temos que:

b² = a² + c²
13² = 5² + c²
169 = 25 + c²
169 – 25 = c²
144 = c²
c = √144
c = 12

Como b é maior, então o foco está no eixo vertical, ou seja (0, 12) e (0, -12).

Por Raul Rodrigues de Oliveira
Professor de Matemática