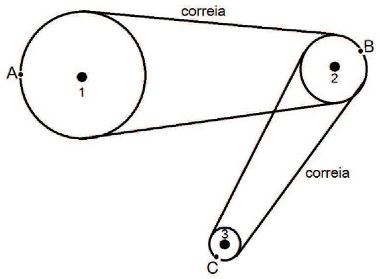
Sistema de Transmissão por Correntes

Matemática

O funcionamento de uma bicicleta é visivelmente simples, mas a movimentação de uma bicicleta através da coroa, corrente, catraca, movimento dos pedais e rodas obedecem a fundamentos da Matemática e da Física. Ao serem movidos, os pedais fazem girar a coroa, que transmite o movimento para a catraca por intermédio de uma corrente, a qual está conectada à roda traseira, colocando a bicicleta em movimento. O percurso completo da roda depende dos diâmetros da coroa, da catraca e da própria roda. Observe o exemplo a seguir:

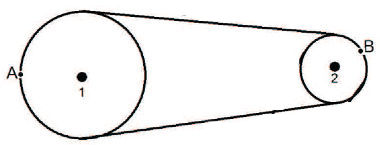
A ilustração a seguir demonstra uma bicicleta com os seguintes diâmetros:

Coroa: 30 cm
Catraca: 10 cm
Roda traseira: 80 cm

Para efetuar tais cálculos utilizaremos a expressão que nos permite calcular o comprimento de uma circunferência: C = 2*π*r, onde π = 3,14 e r o raio.

Vamos determinar o comprimento correspondido a um giro completo da coroa e da catraca

Comprimento da Coroa (diâmetro 30 cm, então raio 15 cm)
C = 2*π*r
C = 2 * 3,14 * 15
C = 94,2 cm

Comprimento da Catraca (diâmetro 10 cm, então raio 5 cm)
C = 2*π*r
C = 2 * 3,14 * 5
C = 31,4

Temos que a razão entre a coroa e a catraca é 94,2 / 31,4 = 3, isto é, enquanto a coroa dá uma volta, a catraca dá três voltas, fazendo com que a roda traseira também dê três voltas completas. Com base nessas informações temos que a distância percorrida pela bicicleta por cada pedalada será:

Diâmetro da roda traseira é igual a 80 cm, portanto, o raio é 40 cm.

C = 3 * (2*π*r)
C = 3 * 2 * 3,14 * 40
C = 753,6 cm ou 7,536 m

Portanto, a bicicleta percorrerá aproximadamente 7,5 metros por pedalada completa.
Vimos que o espaço percorrido por uma bicicleta a cada pedalada será determinado através do diâmetro da coroa, da catraca e da roda traseira, visto que as medidas podem ser diferentes entre os vários modelos de bicicletas existentes.

Não pare agora... Tem mais depois da publicidade ;)

Por Marcos Noé
Graduado em Matemática
Equipe Brasil Escola

Circunferência - Matemática - Brasil Escola

Fundamentos Físicos e Matemáticos no funcionamento de uma bicicleta

Gostaria de fazer a referência deste texto em um trabalho escolar ou acadêmico? Veja:

SILVA, Marcos Noé Pedro da. "Sistema de Transmissão por Correntes "; Brasil Escola. Disponível em: https://brasilescola.uol.com.br/matematica/sistema-transmissao-por-correntes.htm. Acesso em 23 de janeiro de 2021.

Lista de Exercícios

Questão 1

(Fac. Cultura Inglesa-SP) Em uma máquina, quatro roletes estão conectados, por toque ou por correia, sem escorregamentos, como mostra a figura.

Quando o rolete maior gira no sentido horário, com velocidade angular constante, o menor dos roletes gira com uma velocidade angular relativamente

a) igual e de sentido horário.

b) igual e de sentido anti-horário.

c) menor e de sentido horário.

d) maior e de sentido horário.

e) maior e de sentido anti-horário.

Questão 2

(UFU) Uma pessoa dispõe de um motor que gira a 5.000 rpm e acopla-o, usando correias que não escorregam, a três polias (1, 2 e 3), de modo a buscar novas configurações de velocidade e de rotação, diferentes das que o motor proporciona. A, B e C são três pontos marcados nas extremidades das polias 1, 2 e 3, respectivamente. Considere, também, que R_a > R_b > Rc. A figura a seguir representa o acoplamento realizado.