PUBLICIDADE
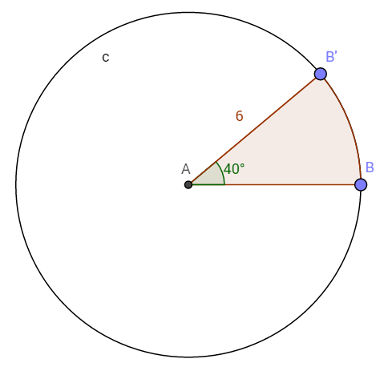
Setor circular corresponde a uma área tomada numa circunferência de centro O e raio R, observe a figura representativa de um setor de α:
.jpg)
A área do setor circular depende diretamente da medida do ângulo central, em razão dessa proporção podemos calcular a área de um setor circular em função do ângulo central aplicando uma regra de três simples. Observe:
| Área | Ângulo Central | |
|
Setor |
A |
α |
|
Círculo Não pare agora... Tem mais depois da publicidade ;) |
π*r² |
360º |
.jpg)
Se a medida do setor for dada em radianos, é preciso lembrar que uma volta completa no círculo é igual a 360º que corresponde a 2π. Dessa forma, a regra de três fica assim:
.jpg)
Exemplo:
Determine a área do setor circular com ângulo central de 30º num círculo de 20 cm de raio.
.jpg){kind=small}
A área do setor circular de 30º corresponde a um setor de π/6 rad, observe os cálculos:
.jpg)
Por Marcos Noé
Graduado em Matemática
Equipe Brasil Escola
