O que são ângulos colaterais internos e externos?

Ângulos colaterais internos e externos são encontrados em duas retas paralelas que foram cortadas por uma reta transversal e possuem propriedades importantes para o desenvolvimento da geometria e para o estudo da Matemática.

As expressões ângulos colaterais internos ou externos estão ligadas à posição que esses ângulos ocupam com relação às retas paralelas e também à reta transversal.

Vale lembrar que duas retas são chamadas paralelas quando não possuem nenhum ponto em comum em toda a sua extensão. Um conjunto com duas ou mais retas paralelas é chamado de feixe de retas paralelas.

Tópicos deste artigo

• 1 - Região interna de duas retas paralelas
• 2 - Região externa de duas retas paralelas
• 3 - Reta transversal
• 4 - Ângulos colaterais internos e externos
• 5 - Propriedades dos ângulos colaterais internos e externos

Região interna de duas retas paralelas

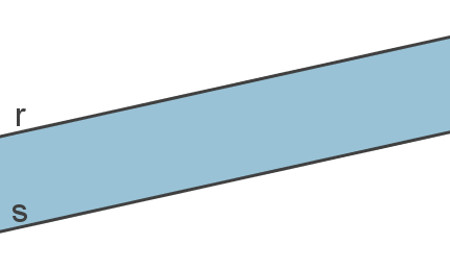
Observe na imagem a seguir a região que é limitada pelas retas paralelas r e s:

Essa região, limitada por duas retas paralelas, é a região interna delas. Os ângulos que estiverem dentro dessa região também são chamados de ângulos internos, assim como qualquer outro elemento, figura geométrica ou objeto.

Região externa de duas retas paralelas

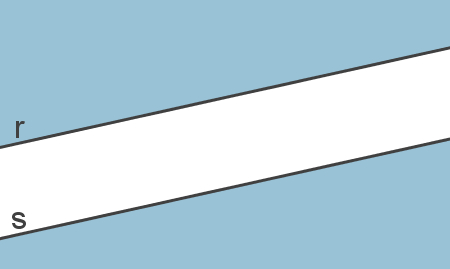
Na imagem a seguir, a região que não é limitada pelas duas retas paralelas, r e s, é externa, isto é, é a região que não é interna.

Essa região em destaque, a região externa, é formada por todos os pontos que não pertencem à região interna de duas retas paralelas. Além disso, qualquer ângulo presente nessa região é chamado ângulo externo.

Reta transversal

Dadas duas retas paralelas, r e s, qualquer reta t que as corte é chamada de reta transversal. Além disso, existe a particularidade que define o seguinte: se uma reta t corta uma reta r, que é paralela a uma reta s, então a reta t também corta a reta s.

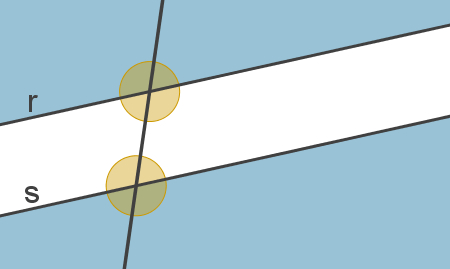
Observe, na imagem abaixo, um exemplo de reta transversal.

Essa reta transversal forma com as duas retas paralelas exatamente oito ângulos. Quatro deles ficam na região interna das retas paralelas e outros quatro ficam na região externa.

Dois ângulos que estejam de um mesmo lado da reta transversal são chamados de colaterais. No caso da figura acima, ângulos à direita da reta transversal são colaterais entre si, e os ângulos à sua esquerda são colaterais entre si.

Ângulos colaterais internos e externos

Com os estudos feitos acima, não resta muito a explicar: dadas duas retas paralelas cortadas por uma transversal, dois ângulos que estão na região interna dessas paralelas e, ao mesmo tempo, são colaterais, são aqueles que são conhecidos como ângulos colaterais internos. Se os ângulos ocupam a região externa das retas paralelas e estão do mesmo lado da reta transversal, então eles são chamados de ângulos colaterais externos.

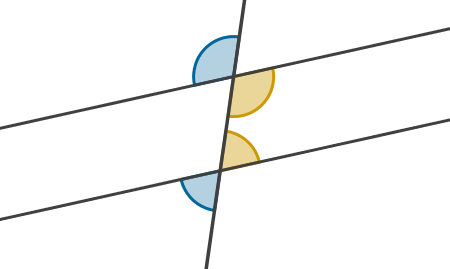
A figura a seguir mostra exemplos de ângulos colaterais externos (em azul) e colaterais internos (em amarelo).

Propriedades dos ângulos colaterais internos e externos

Os ângulos colaterais internos e os ângulos colaterais externos compartilham uma mesma propriedade:

Ângulos colaterais internos são suplementares e

ângulos colaterais externos são suplementares.

Isso significa que a soma entre dois ângulos colaterais internos sempre será igual a 180°, assim como terá o mesmo resultado a soma entre dois ângulos que são colaterais externos.