Área do triângulo por meio da Geometria Analítica

Vamos determinar a área de um triângulo do ponto de vista da geometria analítica. Assim, considere três pontos quaisquer, não colineares, A (x_a, y_a), B (x_b, y_b) e C (x_c, y_c). Como esses pontos não são colineares, ou seja, não estão numa mesma reta, eles determinam um triângulo. A área desse triângulo será dada por:

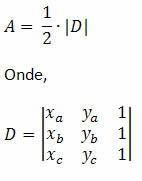
Observe que a área será metade do módulo do determinante das coordenadas dos pontos A, B e C.
 

Exemplo 1. Calcule a área do triângulo de vértices A (4 , 0), B (0 , 0) e C (0 , 6).
Solução: Primeiro passo é fazer o cálculo do determinante das coordenadas dos pontos A, B e C. Teremos:

Assim, obtemos:

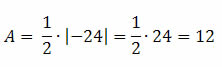
Portanto, a área do triângulo de vértices A (4 , 0), B (0 , 0) e C (0 , 6) é 12.

Exemplo 2. Determine a área do triângulo de vértices A (1, 3), B (2, 5) e C (-2,4).
Solução: Primeiro devemos realizar o cálculo do determinante.

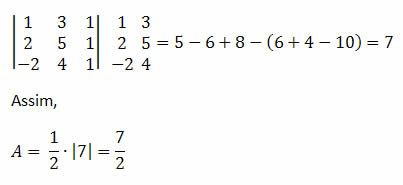
Exemplo 3. Os pontos A (0, 0), B (0, -8) e C (x, 0) determinam um triângulo de área igual a 20. Encontre o valor de x.
Solução: Sabemos que a área do triângulo de vértices A, B e C é 20. Então,

Por Marcelo Rigonatto
Especialista em Estatística e Modelagem Matemática
Equipe Brasil Escola

Geometria Analítica - Matemática - Brasil Escola