Equação geral da reta

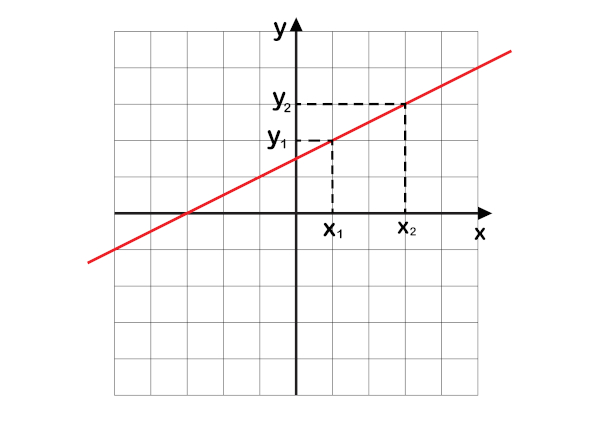
A equação geral da reta é uma das maneiras de descrever a reta de forma algébrica por meio de uma equação. Na geometria analítica, os objetos geométricos são estudados extensivamente, representados no plano cartesiano, e a partir dessa análise é que se busca descrever os objetos geométricos de forma algébrica. Então, a equação geral da reta é uma relação entre uma equação algébrica e a representação geométrica dessa equação, que é uma reta.

A equação geral de uma reta é igual a ax + by + c = 0, em que a, b e c são coeficientes reais e a e b são diferentes de zero. Para encontrar a equação geral de uma reta, é necessário conhecer pelo menos dois pontos dessa equação. Após descobrir esses dois pontos, aplica-se alguns métodos para encontrar a equação da reta que passa por ambos. A representação gráfica de uma reta, conhecendo a sua equação geral, é feita encontrando dois pontos pertencentes a essa reta.

Leia também: Distância entre dois pontos — um dos mais importantes conceitos da geometria analítica

Tópicos deste artigo

• 1 - Resumo sobre equação geral da reta
• 2 - Qual é a equação geral da reta?
• 3 - Como construir a equação geral da reta
  • Método 1 para construir a equação geral da reta 
  • Método 2 para construir a equação geral da reta
• 4 - Gráfico da equação geral da reta
• 5 - Exercícios resolvidos sobre equação geral da reta

Resumo sobre equação geral da reta

• A equação geral da reta é a equação ax + by + c = 0, com a e b diferentes de 0.

• Os pontos pertencentes à reta satisfazem a sua equação geral.

• Podemos encontrar a equação da reta sabendo quais são os dois pontos pertencentes à reta.

• É possível fazer a representação gráfica da reta conhecendo a sua equação geral.

Qual é a equação geral da reta?

A reta é um dos elementos primitivos da geometria, examinada na geometria analítica. Após ter sido estudada a fundo, foi possível descrever o comportamento de uma reta por meio de uma equação geral. A equação geral da reta é, portanto, uma representação algébrica da reta e pode ser descrita pela equação:

Vale ressaltar que a, b e c são números reais, com a e b ≠ 0.

Exemplos:

• 2x + 3y – 4 = 0

• – x + y = 0

• 10x + 5y + 1 = 0

• 2x + y – 0,5 = 0

Como construir a equação geral da reta

Para encontrar a equação da reta, existem dois métodos comuns. Em ambos, é necessário conhecer dois pontos que passam pela reta.

• Método 1 para construir a equação geral da reta 

O primeiro deles é utilizar a condição de alinhamento de três pontos. Para que três pontos do plano cartesiano estejam alinhados, é necessário que o determinante entre esses três pontos seja igual a zero.

Sendo os pontos A e B com coordenadas A(x_A,y_A) e B(x_B,y_B), e P (x,y) um ponto qualquer, para que esses pontos estejam alinhados, temos que:

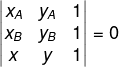
Conhecendo as coordenadas dos pontos A e B, basta igualar o seu determinante a 0 para encontrar a equação geral da reta.

Exemplo:

Encontre a equação geral da reta r que passa pelos pontos A(2,1) e B(4,5).

Resolução:

De início, construiremos o determinante:

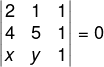
Calculando o determinante, temos que:

10 + 1x + 4y – 5x – 4 – 2y = 0

Agora, juntando os termos semelhantes, encontraremos a equação da reta:

– 4x + 2y – 6 = 0

Então, a equação geral será r: – 4x + 2y – 6 = 0.

• Método 2 para construir a equação geral da reta

Alternativamente, para encontrar a equação geral da reta, utilizaremos duas fórmulas:

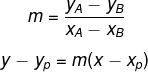
Exemplo:

Encontre a equação geral da reta que passa pelos pontos A(3,1) e B(6,7).

Resolução:

Primeiramente, encontraremos o valor de m:

Agora que encontramos o valor de m e escolhemos o ponto A(3,1), temos que:

y – 1 = 2 (x – 3)

y – 1 = 2x – 6

Igualando-se a 0, temos o seguinte:

y – 1 + 6 – 2x = 0

y + 5 – 2x = 0

Reordenando os termos, obtemos:

– 2x + y + 5 = 0

Leia também: Equação reduzida da reta — o que é e como determiná-la

Gráfico da equação geral da reta

Para representar o gráfico da equação geral da reta, é necessário encontrar os dois pontos pertencentes à reta e representá-los no plano cartesiano.

Exemplo:

Representaremos no plano cartesiano a reta: – 2x + y + 3 = 0

Inicialmente, identificaremos os dois pontos. Escolheremos um valor para x — considerando, por exemplo, x = 2.

x = 2

– 2 · 2 + y + 3 = 0

– 4 + y + 3 = 0

– 1 + y = 0

y = 1

O ponto A(2,1), então, pertence à reta.

Agora, encontraremos outro ponto, considerando x = 3. Se x = 3, temos que:

– 2 · 3 + y + 3 = 0

– 6 + y + 3 = 0

– 3 + y = 0

y = 3

O ponto B(3,3) pertence, então, à reta. Fazendo a representação gráfica, obtemos:

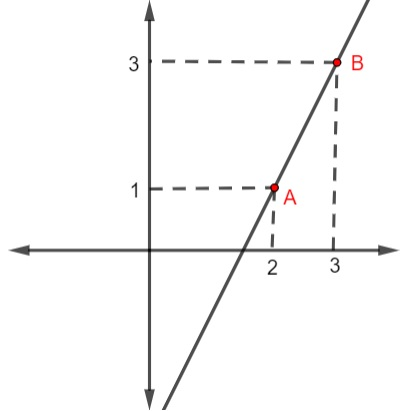
Leia também: Ponto de interseção entre duas retas

Exercícios resolvidos sobre equação geral da reta

Questão 1

Analisando o gráfico a seguir, encontre a equação geral da reta.

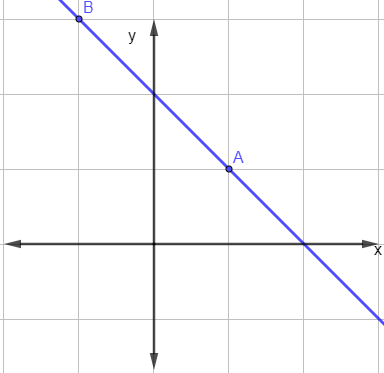
A) – x – y + 2 = 0

B) 3x + 2y – 1 = 0

C) 2x + y – 1 = 0

D) x + 2y – 4 = 0

E) x + y – 2 = 0

Resolução:

Alternativa E

Ao analisar a malha quadriculada, é fácil perceber que as coordenadas são A(1,1) e B(– 1,3). Usando esses dois pontos, temos que:

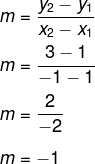
Agora, encontraremos a equação geral da reta, adotando-se o ponto A(1,1):

y – y_p = m(x – x_p)

y – 1 = – 1 (x – 1)

y – 1 = – 1x + 1

y – 1 + x – 1 = 0

x + y – 2 = 0

Questão 2

Dada a reta 2x + y – 4 = 0, marque a alternativa que contenha um ponto pertencente a essa reta.

A) (2,2)

B) (– 2,4)

C) (2,1)

D) (1,2)

Resolução:

Alternativa D

Para encontrar a alternativa correta, é necessário substituir os valores de x e y na equação e verificar se eles atendem à equação.

• A → Não pertence à reta

Substituindo x = 2 e y = 2, temos que:

2 · 2 + 2 – 4 = 0

4 + 2 – 4 = 0

6 – 4 = 0

2 = 0 (sentença falsa)

• B → Não pertence à reta

x = – 2 e y = 4

2 · (– 2) + 4 – 4 = 0

– 4 + 4 – 4 = 0

4 = 0 (sentença falsa)

• C → Não pertence à reta

x = 2 e y = 1

2 · 2 + 1 – 4 = 0

4 + 1 – 4 = 0

1 = 0 (sentença falsa)

• D → Pertence à reta

x = 1 e y = 2

2 · 1 + 2 – 4 = 0

2 + 2 – 4 = 0

0 = 0 (sentença verdadeira)

O ponto (1,2) pertence, então, à reta.

 

Por Raul Rodrigues de Oliveira
Professor de Matemática