Cálculo do coeficiente angular

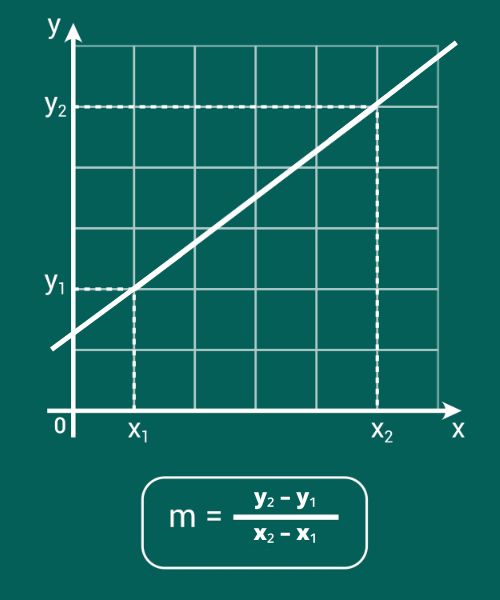
O cálculo do coeficiente angular de uma reta é feito, principalmente, a partir das coordenadas de dois pontos. Dados dois pontos de uma reta, o coeficiente angular é a razão entre a diferença de coordenadas no eixo das ordenadas e a diferença de coordenadas no eixo das abscissas.

O coeficiente angular de uma reta é um número que indica a inclinação de uma reta em relação à horizontal e influencia no comportamento da reta para valores crescentes de x. Dada a equação reduzida de uma reta, o coeficiente angular é o número que multiplica a variável x. Também é possível determinar o coeficiente angular de outras duas maneiras: a partir do ângulo entre a reta e o eixo horizontal ou a partir das coordenadas de dois pontos da reta.

Leia também: Qual é a equação geral de uma reta?

Tópicos deste artigo

• 1 - Resumo sobre o cálculo do coeficiente angular
• 2 - O que é coeficiente angular?
• 3 - Fórmulas do coeficiente angular de uma reta
  • → Fórmula para calcular o coeficiente angular a partir de dois pontos da reta
  • → Fórmula para calcular o coeficiente angular a partir do ângulo θ entre a reta e a horizontal
• 4 - Como calcular o coeficiente angular de uma reta?
• 5 - Diferenças entre coeficiente angular e coeficiente linear
• 6 - Exercícios sobre coeficiente angular

Resumo sobre o cálculo do coeficiente angular

• O coeficiente angular de uma reta é um número que indica a inclinação de uma reta em relação à horizontal e influencia no comportamento da reta para valores crescentes de x.
• Na reta de equação y = mx +n , m ≠ 0, os números m e n são, respectivamente, os coeficientes angular e linear.
• Se \(A=\left(x_1,y_1\right)\)e \(B=\left(x_2,y_2\right)\) são pontos de uma reta, seu coeficiente angular m pode ser calculado pela expressão:

\(m=\frac{y_2-y_1}{x_2-x_1}\)

• Se θ é o ângulo entre a reta e a horizontal, o coeficiente angular m pode ser calculado pela expressão:

\(m=tg\ \theta\)

• Enquanto o coeficiente angular indica a inclinação da reta, o coeficiente linear expressa a coordenada vertical em que a reta cruza o eixo y.

O que é coeficiente angular?

O coeficiente angular é um número que está relacionado ao ângulo formado entre a reta e a horizontal, descreve a inclinação da reta e pode ser determinado pela equação reduzida. Considere a reta de equação y = mx + n, m ≠ 0, em que m e n são números (constantes) reais. A constante m é o coeficiente angular dessa reta e a constante n é o coeficiente linear. Uma característica importante do coeficiente angular é que ele determina se a reta é crescente ou decrescente: se m > 0, a reta é crescente, e, se m < 0, a reta é decrescente.

E como podemos calcular o coeficiente angular de uma reta sem conhecer sua equação? É o que veremos adiante.

Fórmulas do coeficiente angular de uma reta

→ Fórmula para calcular o coeficiente angular a partir de dois pontos da reta

Dados os pontos \(A=\left(x_1,y_1\right) e\ B=\left(x_2,y_2\right)\) de uma reta, tem-se que o coeficiente angular m é dado pela razão entre a diferença das coordenadas no eixo \(y \left(y_2-y_1\right)\)e a diferença das coordenadas no eixo \(x \left(x_2-x_1\right)\):

\(m=\frac{y_2-y_1}{x_2-x_1}\)

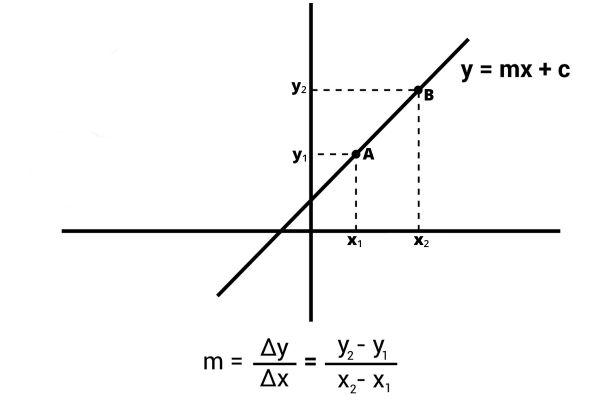
→ Fórmula para calcular o coeficiente angular a partir do ângulo θ entre a reta e a horizontal

Seja θ o ângulo entre a reta e a horizontal, assim, o coeficiente angular m da reta é a tangente de θ:

\(m=tg\ \theta\)

Observação 1: Note que as duas formas de calcular estão relacionadas. Traçando uma reta horizontal (paralela ao eixo x) pelo ponto \(\left(x_1,y_1\right)\), temos um triângulo retângulo cujos catetos medem \(x_2-x_1 e\ y_2-y_1\) e a hipotenusa é o segmento AB. O ângulo entre o cateto horizontal e a hipotenusa é θ, portanto, sua tangente é a razão entre \(y_2-y_1\) (medida do cateto oposto) e \(x_2-x_1\) (medida do cateto adjacente). Dessa forma, temos:

\(m=\frac{y_2-y_1}{x_2-x_1}=tg\ \theta\)

Observação 2: Existe uma relação entre os coeficientes lineares de duas retas paralelas e entre os coeficientes lineares de duas retas perpendiculares.

• Se duas retas r e s são retas paralelas, o coeficiente angular de r \((m_r)\) é igual ao coeficiente linear de s \((m_s)\).

\(m_r=m_s\)

• Se duas retas r e s são perpendiculares, o coeficiente angular de r \((m_r)\) é igual ao oposto do inverso multiplicativo do coeficiente linear de s \((m_s)\).

\(m_r=-\frac{1}{m_s}\)

Como calcular o coeficiente angular de uma reta?

Se a equação da reta for conhecida, basta identificar a constante que multiplica a variável x para obter o coeficiente angular. Do contrário, devemos utilizar as fórmulas estudadas no tópico anterior \((m=\frac{y_2-y_1}{x_2-x_1} e m=tg\ \theta)\).

• Exemplo 1

Qual o coeficiente angular da reta que passa pelos pontos A = (11, 2) e B = (13, 3)?

Resolução:

Considerando as coordenadas de A como \(x_1\ e \ y_1\) e as coordenadas de B como \(x_2\ e \ y_2\) e aplicando a fórmula, temos que:

\(m=\frac{y_2-y_1}{x_2-x_1}=\frac{3-2}{13-11}=\frac{1}{2}=0,5\)

• Exemplo 2

Qual o coeficiente angular da reta que forma um ângulo de 135° com o eixo x?

Resolução:

Como θ = 135°, temos que:

\(m=tg\ \theta=tg\ 135°= - tg 45°=-1\)

Diferenças entre coeficiente angular e coeficiente linear

Em uma reta y = mx + n, a constante m é o coeficiente angular e a constante n é o coeficiente linear. Enquanto o coeficiente angular indica a inclinação da reta, o coeficiente linear expressa a coordenada vertical em que a reta cruza o eixo y. Note que para x = 0 temos n = y. Assim, (0, n) é o ponto em que a reta y = mx + n intercepta o eixo y.

• Exemplo:

Na reta y = 3x -2, o coeficiente angular é 3 e o coeficiente linear é -2. O gráfico dessa reta cruza o eixo y no ponto 0,-2.

Acesse também: Qual é a equação paramétrica de uma reta?

Exercícios sobre coeficiente angular

Questão 1

Qual o coeficiente angular da reta com equação \(y=\frac{x+2}{2}\)?

A) 0,5

B) 1

C) 1,5

D) 2

E) 2,5

Resolução:

Alternativa A

Observe que podemos escrever:

\(y=\frac{x+2}{2}=\frac{x}{2}+\frac{2}{2}=\frac{1}{2}x+1=0,5x+1\)

Portanto, o coeficiente angular dessa reta é 0,5.

Questão 2

O ângulo entre as retas s e t é 90° e o coeficiente angular de s é – 4. O coeficiente angular de t é igual a

A) 0,05.

B) 0,25.

C) 0,55.

D) 0,75.

E) 0,95.

Resolução:

Alternativa B

Como as retas s e t são perpendiculares, temos que:

\(m_t=-\frac{1}{m_s}=-\frac{1}{-4}=\frac{1}{4}=0,25\)

Fontes

BOULOS, P.; CAMARGO; I. de. Geometria Analítica: um tratamento vetorial. 3 ed. São Paulo: Pearson, 2006.

LIMA, E. L. Geometria Analítica e Álgebra Linear. Rio de Janeiro: Impa, 2014.