Os tipos de fração que existem podem ser compreendidos como os casos particulares de fração. A representação de um número como uma fração é bastante comum, pois quando o número não é exato, recorremos à fração para representá-lo. Sendo assim, existem alguns casos especiais de fração, que são:
-
fração própria;
Anuncie aqui -
fração imprópria;
-
fração aparente;
-
fração irredutível;
-
fração mista.
Uma fração é considerada própria quando o numerador é menor que o denominador e imprópria quando o numerador é maior que o denominador. A fração aparente é aquela cuja divisão entre o numerador e o denominador tem como resposta um número inteiro. Uma fração é classificada como irredutível se não existir nenhum número que divida o numerador e o denominador simultaneamente. Já a fração mista é um outro jeito de representar uma fração imprópria, separando a parte inteira da parte fracionária.
Leia também: Tipos de matrizes — as classificações das matrizes de acordo com sua organização
Tópicos deste artigo
- 1 - Videoaula sobre tipos de fração
- 2 - O que é fração?
- 3 - Tipos de fração
- 4 - Conversão de fração mista e imprópria
- 5 - Exercícios resolvidos sobre fração
Videoaula sobre tipos de fração
O que é fração?
Conhecemos como fração uma maneira de representar uma quantidade de partes ou divisões de algo inteiro, sendo que a parte de cima representa as partes obtidas e a parte de baixo representa as partes em que o todo foi dividido.
Tipos de fração
As frações podem ser classificadas de acordo com as suas características. Veremos cada um dos seus tipos a seguir.
→ Fração própria
Uma fração é classificada como própria quando seu numerador é menor que o denominador. Veja os exemplos a seguir.
\(\frac{1}{2}\)
\(\frac{5}{9}\)
\(\frac{6}{13}\)
→ Fração imprópria
A fração imprópria é o contrário da fração própria. Uma fração é conhecida como imprópria quando o numerador é maior que o denominador. Veja os exemplos a seguir.
\(\frac{13}{5}\)
\(\frac{8}{7}\)
\(\frac{15}{11}\)
→ Fração aparente
A fração é classificada como aparente quando a divisão entre o numerador e o denominador é igual a um número inteiro. Veja os exemplos a seguir.
\(\frac{12}{4}\)
Sabemos que 12 é divisível por 4 e que \(\frac{12}{4}=3\), então essa é uma fração aparente.
357
Sabemos que 35 é divisível por 7 e que \( \frac{35}{7}=5\), então essa é uma fração aparente.
→ Fração irredutível
Uma fração é conhecida como irredutível quando o numerador e o denominador possuem seu menor valor possível. Veja exemplos a seguir.
\(\frac{3}{5}\)
\(\frac{2}{9}\)
\(\frac{13}{18}\)
Simplificação de frações
Quando a fração não está na sua forma irredutível, é possível realizar a simplificação dessa fração. Se o numerador e o denominador são múltiplos de um mesmo número, podemos dividi-los pelo divisor comum entre eles até que a fração se torne irredutível.
Exemplo:
\(\frac{12}{15}\)
Sabemos que tanto 12 quanto 15 são divisíveis por 3, logo:
\(\frac{{12}^{:3}}{{15}_{:3}}=\frac{4}{5}\)
A forma irredutível dessa fração é, portanto, \(\frac{4}{5}\).
→ Fração mista
A fração mista é uma segunda forma de representar uma fração imprópria, pois é composta pela parte inteira do número seguida da parte fracionária. Veja os exemplos a seguir.
\(9\frac{3}{4}\)
\(3\frac{2}{5}\)
\(6\frac{1}{2}\)
Conversão de fração mista e imprópria
Uma fração mista pode ser representada como uma fração imprópria, e uma fração imprópria pode ser representada como uma fração mista.
→ Conversão de uma fração mista em uma fração imprópria
Para realizar a conversão, basta calcular a soma entre a parte inteira e a parte fracionária da fração.
Exemplo:
\(5\frac{2}{9}\)
\(5+\frac{2}{9}\)
Calculando o MMC (mínimo múltiplo comum), temos que:
\(\frac{45+2}{9}\)
Assim, a representação da fração mista \(5\frac{2}{9} \) como uma fração imprópria é:
\(\frac{47}{9}\)
→ Conversão de uma fração imprópria em uma fração mista
Para realizar a conversão, basta calcular a divisão entre o numerador e o denominador do número. O quociente da divisão será a parte inteira, o resto da divisão será o numerador da parte fracionária e o denominador permanecerá o mesmo.
Exemplo:
\(\frac{47}{9}\)
Faremos primeiramente a divisão de 47 por 9:
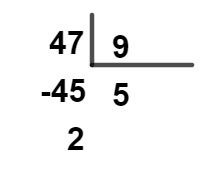
Esse número possui 5 partes inteiras mais 2/9, logo a representação em número misto é:
\(5\frac{2}{9}\)
Saiba mais: Operações com frações — como fazer?
Exercícios resolvidos sobre fração
Questão 1
A forma irredutível da fração \(\frac{18}{36}\) é igual a:
A) \( \frac{2}{4}\)
B) \( \frac{1}{2}\)
C) \( \frac{4}{15}\)
D) \( \frac{1}{3}\)
E) \( \frac{8}{15}\)
Resolução:
Alternativa B
Podemos simplificar a fração dividindo o numerador e o denominador por 18:
\(\frac{{18}^{:18}}{{36}_{:18}}=\frac{1}{2}\)
Questão 2
Analise a fração a seguir:
\(\frac{28}{18}\)
Essa fração pode ser classificada como:
A) fração própria
B) fração imprópria
C) fração aparente
D) fração irredutível
E) fração mista
Resolução:
Alternativa B
Quando o numerador é maior que o denominador, a fração é classificada como própria. Perceba que a divisão de 28 por 18 não resulta em um número exato, logo a fração não pode ser aparente. Ademais, tanto 28 quanto 18 são divisíveis por 2, logo ela não é irredutível. Assim, trata-se de uma fração própria.
Por Raul Rodrigues de Oliveira
Professor de Matemática