Fluidos

Os fluidos são, principalmente, gases e líquidos que devido à tensão de cisalhamento (tensão ocorrida quando se aplica uma força paralela ao movimento do fluido contido em uma superfície) conseguem escoar naturalmente. Eles possuem algumas propriedades, como densidade, que varia de acordo com a distribuição da massa pelo volume, e pressão, que é a força aplicada sobre uma área.

Além disso, os fluidos são regidos por alguns princípios, como a lei de Stevin, que aborda a diferença de pressões em alturas distintas; o princípio de Pascal, que fala sobre a pressão em um ponto gerar a mesma variação de pressão em todo o restante do líquido; e o teorema de Arquimedes, que introduz o conceito de empuxo, uma força atuante sobre corpos imersos em líquidos que afundam ou boiam de acordo com a relação entre a força peso com a força de empuxo.

Veja também: O princípio de Pascal e o funcionamento dos pistões hidráulicos

Tópicos deste artigo

• 1 - Resumo sobre fluidos
• 2 - Características dos fluidos
• 3 - Massa específica e os fluidos
• 4 - Pressão e os fluidos
• 5 - Princípio de Stevin e os fluidos
• 6 - Vasos comunicantes e os fluidos
• 7 - Teorema de Pascal
• 8 - Teorema de Arquimedes
  • → Videoaula sobre empuxo
• 9 - Exercícios resolvidos sobre fluidos

Resumo sobre fluidos

• Fluidos são líquidos e gases que têm a capacidade de fluírem ou escoarem com grande facilidade.

• Massa específica mede a capacidade de um objeto de flutuar ou afundar dependendo da distribuição de sua massa e volume.

• Pressão ocorre quando uma força é aplicada sobre uma superfície plana.

• O princípio de Stevin relaciona a diferença de pressão entre pontos de um líquido com suas diferentes alturas.

• O princípio de Pascal determina que a pressão sofrida em um ponto de um líquido é repassada para todo o restante, sofrendo todos com a mesma variação de pressão.

• Nos vasos comunicantes, a altura dos líquidos é a mesma, independentemente do formato da ramificação. Porém, se a densidade dos líquidos contidos forem diferentes, a altura muda.

• O teorema de Arquimedes fala do empuxo, que ocorre em corpos imersos em líquidos. Um corpo imerso afunda ou flutua dependendo da relação existente entre a força de empuxo e a força peso.

Características dos fluidos

Fluidos são substâncias líquidas ou gasosas que têm a propriedade de se deformarem facilmente quando submetidas à tensão de cisalhamento, causada pela aplicação de uma força paralela ao movimento do fluido em uma superfície. Por menor que seja, ela consegue provocar o escoamento do líquido.

O líquido possui volume definido, mas sua forma varia de acordo com o recipiente em que foi inserido. Já o gás não possui volume definido e pode expandir enquanto houver espaço. Ambos são tratados como fluidos por conseguirem se deformar sem grandes dificuldades.

Massa específica e os fluidos

Massa específica, ou densidade, é uma grandeza física que mede a capacidade de um fluido ou sólido flutuar ou afundar em outros fluidos dependendo da sua distribuição de massa e volume. Comumente, se ouve que quanto mais massa um corpo tiver, mais irá afundar, mas nem sempre isso ocorre.

Isso pode ser percebido no fato de um sólido como o isopor flutuar na água, já o ferro afundar, por causa das suas densidades. O mesmo ocorre com os líquidos, que quando combinados podem se manter em diferentes fases, devido à sua alta ou baixa densidade, conforme a imagem a seguir.

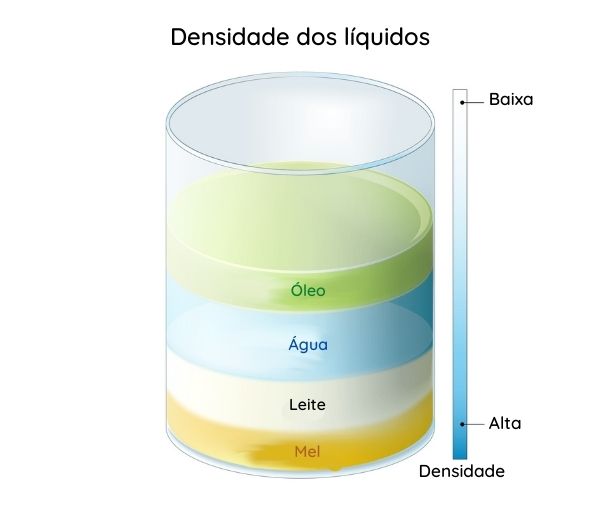
Podemos calcular a massa específica por meio da fórmula:

\(d=\frac{m}{V}\)

• \(d\) é a densidade, medida em \([kg/m^3]\).

• \(m \) é a massa, medida em quilogramas \(\left[kg\right]\).

• \(V\) é o volume, medido em \(\left[m^3\right]\).

Pressão e os fluidos

Pressão é uma grandeza física que ocorre quando aplicamos uma força sobre uma superfície plana. Quanto mais fundo nadamos ou quanto mais alto estamos, maior será a pressão sentida.

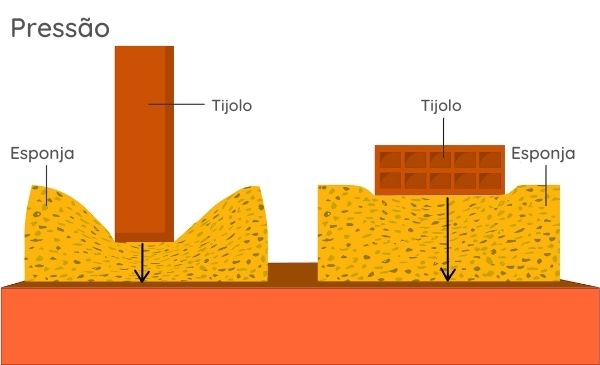
Conseguimos calcular a pressão por meio da fórmula:

\(p=\frac{\vec{F}}{A}\)

• \(p\) é a pressão, medida em Pascal \([Pa]\).

• \(\vec{F}\) é a força, medida em Newton \(\left[N\right]\).

• \(A\) é a área da superfície, medida em \(\left[m^2\right]\).

Importante: Conversões da unidade de medida de pressão:

\(1\ atm=1,01\ \bullet{10}^5\ Pa=760\ mmHg=14,7\ lb/{pol}^2\)

Princípio de Stevin e os fluidos

O princípio de Stevin, desenvolvido por Simon Stevin (1548–1620), trata da diferença de pressão entre pontos de um líquido em diferentes alturas. Sua principal aplicação se dá em relação aos vasos comunicantes, recipiente formado por diversas ramificações que interagem entre si. 

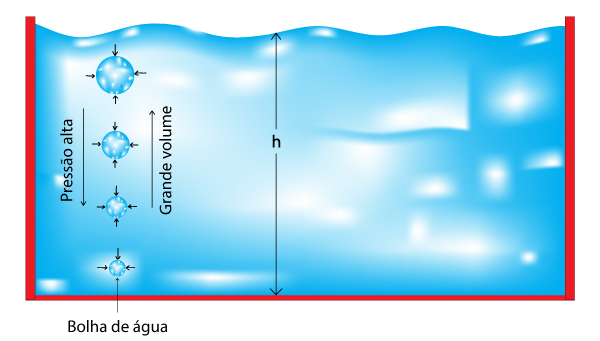
O enunciado da lei de Stevin diz o seguinte:

“A diferença de pressão entre os dois pontos de um líquido homogêneo em equilíbrio é constante, dependendo apenas do desnível entre esses pontos.”

Seu cálculo se dá por meio da fórmula:

\(∆p=d∙g∙∆h\)

Ou

\(p-p_o=d\bullet g\bullet∆h\)

• \(∆p \) é a pressão manométrica, medida em Pascal \([Pa]\).

• \(p\) é a pressão absoluta ou total, medida em Pascal \([Pa]\).

• \(p_o\) é a pressão atmosférica, medida em Pascal \([Pa]\).

• g é a gravidade, medida em \([m{/s}^2]\).

• h é a altura, medida em metros \([m]\).

Leia também: O que é uma transformação isovolumétrica?

Vasos comunicantes e os fluidos

O princípio dos vasos comunicantes é um dos resultados obtidos a partir da lei de Stevin que diz que se há um reservatório formado por duas ou mais ramificações conectadas entre si, o líquido contido, desde que seja de mesma densidade, subirá em todas na mesma altura e conterá a mesma pressão sobre cada uma delas.

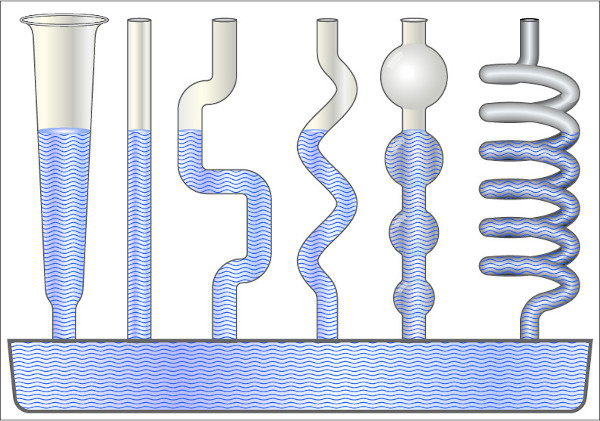
Já para o caso de dois líquidos com diferentes densidades contidos em um recipiente no formato de U, as pressões exercidas neles e suas alturas são diferentes.

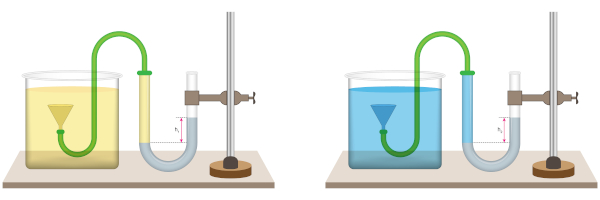
Para esse caso, podemos fazer o cálculo utilizando a fórmula:

\(\frac{H_1}{H_2}=\frac{d_2}{d_1}\)

Ou

\(H_1\bullet d_1=H_2\bullet d_2\)

• \(H_1 \) e \( H_2\) são as alturas relacionadas às áreas, medidas em metros \([m]\).

• \(d_1\) e \(d_2\) são as densidades dos fluidos, medidas em \([kg/m^3]\).

Teorema de Pascal

Baseado na lei de Stevin, que trata da variação de pressão entre pontos em um líquido a diferentes alturas, Blaise Pascal (1623–1662) aplicou a mesma lógica à prensa hidráulica, máquina simples constituída por dois cilindros conectados que possuem um fluido em seu interior, conforme a imagem a seguir.

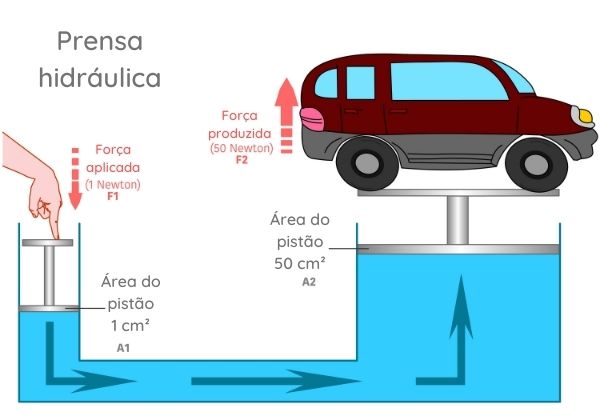
O enunciado do Teorema de Pascal diz o seguinte:

“Se produzirmos uma variação de pressão em um ponto de um líquido em equilíbrio, essa variação se transmite a todo o líquido, ou seja, todos os pontos do líquido sofrem a mesma variação de pressão.”

Podemos fazer o cálculo utilizando a fórmula:

\(\frac{{\vec{F}}_1}{A_1}=\frac{{\vec{F}}_2}{A_2}\)

Ou

\(\frac{A_1}{A_2}=\frac{H_2}{H_1}\)

• \({\vec{F}}_1 \) e \({\vec{F}}_2 \) são as forças aplicada e recebida, respectivamente, medidas em Newton \([N]\).

• \(A_1\) e \(A_2 \) são as áreas relacionadas à aplicação das forças, medidas em \([m^2]\).

• \(H_1\) e \(H_2\) são as alturas relacionadas às áreas, medidas em metros \([m]\).

Saiba mais: Sete erros mais comuns cometidos no estudo de Física

Teorema de Arquimedes

O teorema de Arquimedes diz respeito ao empuxo, descoberto por Arquimedes (287 a.C.–212 a.C.), que é uma força hidrostática atuante em corpos submersos em fluidos total ou parcialmente. De acordo com o historiador Vitrúvio (80 a.C–15 a.C.), o rei de Siracusa Herão acreditava ter sido enganado quanto ao material da sua coroa e pediu a Arquimedes para investigar, conforme identifica-se no trecho abaixo, retirado do livro Curso de Física Básica: Fluidos, Oscilações e Ondas, Calor:

“Enquanto Arquimedes pensava sobre o problema, chegou por acaso ao banheiro público e lá, sentado na banheira, notou que a quantidade de água que transbordava era igual à porção imersa de seu corpo. Isso lhe sugeriu um método de resolver o problema, e sem demora saltou alegremente da banheria e, correndo nu para casa, gritava bem alto que tinha achado o que procurava. Pois, enquanto corria, gritava repetidamente em grego ‘Eureka! Eureka!’ (‘Achei! Achei!’).”

O enunciado geral do princípio de Arquimedes diz o seguinte:

“Um corpo total ou parcialmente imerso em um fluido recebe dele um empuxo igual e contrário à força peso da porção de fluido deslocada, aplicado no centro de gravidade dessa porção.”

O empuxo possui direção vertical, sentido para cima, contrário à força peso, e sua intensidade é calculada por meio da fórmula:

\(\vec{E}=d_f\bullet V_{fd}\bullet\vec{g}\)

• \(E\) é a força de empuxo, medida em Newton \([N]\).

• \(d_f\) é a densidade do fluido, medida em \([kg/m^3]\).

• \(V_{fd}\) é o volume do fluido deslocado, medido em \(\left[m^3\right]\).

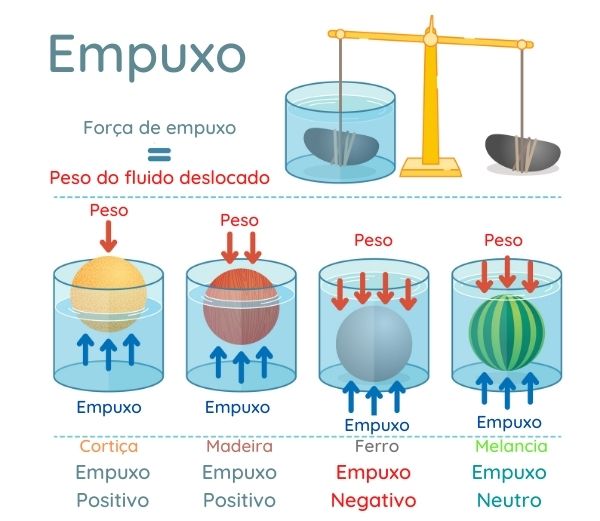
Podemos comparar a força de empuxo com a força peso:

• Se a força empuxo (\(E\)) for maior que a força peso (\(P\)), o corpo flutua.

• Se a força empuxo (\(E\)) for igual a força peso (\(P\)), o corpo não sobe nem desce; permanece no mesmo lugar.

• Se a força empuxo (\(E\)) for menor que a força peso (\(P\)), o corpo afunda.

→ Videoaula sobre empuxo

Exercícios resolvidos sobre fluidos

Questão 1

(Fesp - SP) Um cubo oco de alumínio apresenta 100 g de massa e volume de 50 cm³ . O volume da parte vazia é de 10 cm³. A densidade do cubo e a massa específica do alumínio são, respectivamente:

A) \(0,5\ g/cm³ e 0,4 g/cm³\)

B) \(2,5\ g/cm³ e 2,0 g/cm³\)

C) \(0,4g/cm^3e0,5g/cm^3\)

D) \(2,0\ g/cm³ e 2,5 g/cm³\)

E) \(2,0\ g/cm³ e 10,0 g/cm³ \)

Resolução:

Alternativa D

Primeiramente, calcularemos a densidade do cubo:

\(d=\frac{m}{V}\)

\(d=\frac{100}{50}\)

\(d=2\ g/{cm}^3\)

Já a massa específica do alumínio será:

\(d=\frac{m}{V}\)

\(d=\frac{100}{50-10}\)

\(d=\frac{100}{40}\)

\(d=2,5g/{cm}^3\)

Questão 2

(Aman) Um tanque contendo \(5,0\ x\ {10}^3\) litros de água tem 2,0 metros de comprimento e 1,0 metro de largura. Sendo \(g\ =\ 10\ m{/s}^2\), a pressão hidrostática exercida pela água no fundo do tanque vale:

A) \(2,5\bullet{10}^4\ Nm^{-2}\)

B) \(2,5\bullet{10}^1\ Nm^{-2}\)

C) \(5,0\bullet{10}^3\ Nm^{-2}\)

D) \(5,0\bullet{10}^4\ Nm^{-2}\)

E) \(2,5\bullet{10}^6\ Nm^{-2}\)

Resolução:

Alternativa A

De início, mudaremos a unidade de medida do volume de litros para \(m^3\):

\(V=5\bullet{10}^3L=5{\ m}^3\)

A altura será dada por:

\(5=1\bullet2\bullet h\)

\(5=2\bullet h\)

\(\frac{5}{2}=h\)

\(2,5=h\)

Para calcularmos a pressão hidrostática exercida pela água no fundo do tanque, utilizaremos a lei de Stevin:

\(p=d\bullet g\bullet h\)

Considerando a densidade da água como \({1000\ kg/m}^3\) e a gravidade como \(10m/s^2\), encontraremos:

\(p=1000\bullet10\bullet2,5\)

\(p=2,5\bullet{10}^4\ Pa=2,5\bullet{10}^4\ Nm^{-2}\)

Por Pâmella Raphaella Melo
Professora de Física