Força peso de um corpo é a força gravitacional, exclusivamente atrativa, produzida por um segundo corpo de grande massa, como a Terra, a Lua ou o Sol, por exemplo. De acordo com a lei da gravitação universal, dois corpos que contenham massa atraem-se com uma força inversamente proporcional ao quadrado da distância que os separa.
Força peso, força gravitacional ou simplesmente peso são fundamentalmente a mesma coisa, no entanto, é bastante comum que confundamos os conceitos de peso e massa, que são diferentes. Enquanto o peso é uma força, medida em newtons (N), a massa de um corpo é a quantidade de matéria nele contida, medida em quilogramas (kg).
Acesse também: Massa x peso
Tópicos deste artigo
- 1 - O que é peso na física?
- 2 - Fórmula da força peso
- 3 - Peso e terceira lei de Newton
- 4 - Peso e força normal
- 5 - Trabalho da força peso
- 6 - Força peso e gravitação
- 7 - Exercícios sobre a força peso
O que é peso na física?
Peso é uma força que surge da atração gravitacional entre dois corpos constituídos de massa, sabendo disso, podemos calculá-lo pela multiplicação entre a massa de um desses corpos, medida em quilogramas, e a aceleração da gravidade local, em m/s². Enquanto a nossa massa permanece invariável quando nos deslocamos entre dois pontos com diferentes gravidades, nosso peso muda.
Por exemplo: um objeto de 10 kg na Terra, onde a gravidade é de aproximadamente 9,8 m/s², terá um peso de 98 N, enquanto na Lua, onde a gravidade é de 1,6 m/s², o peso desse corpo seria de apenas 16 N.
Veja também: Entenda por que não sentimos a Terra girar
Fórmula da força peso
A fórmula usada para calcular a força peso é esta, confira:
![]()
P - peso (N)
m - massa (kg)
g - gravidade local (m/s²)
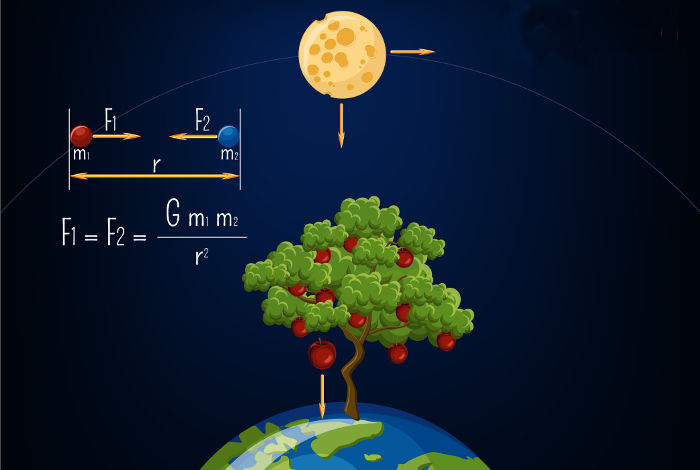
O peso, por tratar-se de uma força, é vetorial. Essa força sempre aponta em direção ao centro da Terra e é responsável por manter-nos presos em sua superfície. De modo similar, o Sol atrai a Terra em direção ao seu centro, ou seja, essa estrela exerce uma força peso sobre o nosso planeta.
A razão pela qual a Terra não cai em direção ao Sol é a grande velocidade na qual o nosso planeta orbita em torno da estrela. Além disso, por ser uma força que aponta sempre para o centro da trajetória da Terra em torno do Sol, a força gravitacional que este faz sobre aquela não é capaz de afetar o módulo da velocidade de translação, somente o seu sentido.
Peso e terceira lei de Newton
De acordo com a terceira lei de Newton, quando exercemos uma força contra um corpo, recebemos dele de volta a mesma força, na mesma intensidade e direção, porém com sentido oposto. Aplicada no contexto do peso, essa lei indica que a força que a Terra faz sobre nós para baixo é feita sobre a Terra para cima, e isso está correto. Se a Terra é capaz de puxar-nos em direção ao seu centro, nós também fazemos sobre ela uma força de mesma intensidade, mas em sentido contrário.
O motivo de nós cairmos em direção à Terra, e não o contrário, é a inércia: a massa da Terra é muito maior do que as nossas massas, por isso, a sua tendência de permanecer em repouso é muito maior, de modo que a aceleração adquirida por ela, graças à força peso que exercemos, é ínfima, quase nula.
Leia também: O que aconteceria se a Terra parasse de girar?
Peso e força normal
Força normal e força peso são frequentemente confundidas como um par de ação e reação. No entanto, essas forças atuam sobre o mesmo corpo e, por isso, violam a condição estabelecida pela terceira lei de Newton. De fato, a força normal é uma força de reação à compressão que é feita sobre alguma superfície, e não à força peso.
Trabalho da força peso
O trabalho exercido por uma força mede a quantidade de energia que foi transferida entre dois ou mais corpos. A fórmula que é usada para o cálculo do trabalho da força peso é esta, confira:
![]()
τ - trabalho (J - joule)
P - peso (N - newton)
d - deslocamento (m - metro)
θ - ângulo entre a força e peso
A fórmula mostra-nos que a quantidade de trabalho realizada pela força peso depende da intensidade dessa força multiplicada pelo deslocamento, mas também do ângulo θ, formado entre o deslocamento e a força peso. Vamos conferir alguns casos especiais:
-
Quando o ângulo θ for igual a 0º: Se a força peso e o deslocamento formarem um ângulo de 0 graus, a força peso será positiva, isto é, o trabalho da força peso produzirá um aumento de energia cinética, como quando um objeto cai em direção ao centro da Terra.
-
Quando o ângulo θ for igual a 180º: Nesse caso, a força peso e o deslocamento estão opostos, como quando jogamos um objeto para cima, aqui na Terra: quando o fazemos, o corpo perde energia cinética, uma vez que o trabalho é negativo, já que o cosseno de 180º equivale a -1.
-
Quando o ângulo θ for igual a 90º: Uma vez que o cosseno de 90º é 0, a força peso não realizará trabalho em direções perpendiculares a ela, como quando fazemos uma caminhada na horizontal. Nesse caso, o peso do corpo não produzirá qualquer alteração em sua energia cinética.
Não pare agora... Tem mais depois da publicidade ;)
Veja também: Confira o que é mais importante sobre as três leis de Newton
Força peso e gravitação
A gravitação universal é uma das leis de Newton, essa lei afirma que todos os corpos dotados de massa atraem-se em pares, com a mesma força. Além disso, essa lei indica que a força de atrativa entre os corpos é proporcional ao produto de suas massas e inversamente proporcional à distância que os separa elevada ao quadrado. Confira a fórmula da gravitação universal:
![]()
FG - força gravitacional (N)
G - constante de gravitação universal (6,674.10-11 N.m²/kg²)
M e m - massas dos corpos (kg)
r - distância entre os corpos (m)
A primeira fórmula mostrada, à esquerda, é o que chamamos de lei da gravitação universal, nela, é possível perceber que, além da massa m, existe o termo GM/r², esse termo é usado para calcular a aceleração da gravidade produzida por um corpo de massa M, em um ponto que se encontra a uma distância r de seu centro de massa. Além disso, a letra G é uma constante de proporcionalidade que se aplica a todos os corpos.
Por meio da fórmula à direita, mostrada na figura anterior, é possível calcular a gravidade da Terra em sua superfície. Para tanto, faremos uso da massa da Terra (M = 5,972.1024 kg), o raio equatorial da Terra (r = 6,371.106 m) e a constante de gravitação (G = 6,674.10-11 N.m²/kg²), e assim poderemos estimar qual deve ser a gravidade da Terra em sua superfície:

O resultado mostra que a teoria da gravitação universal de Isaac Newton é capaz de prever o módulo da gravidade da Terra, e os seus resultados são compatíveis àqueles medidos pelos instrumentos mais precisos.
Veja também: Por que a Lua não cai na Terra?
Exercícios sobre a força peso
Questão 1) Em relação aos conceitos de peso e massa, assinale a alternativa INCORRETA:
a) O peso é calculado pela massa do corpo multiplicada pela aceleração da gravidade local.
b) Peso e massa são grandezas físicas diferentes.
c) A força peso aponta para baixo.
d) Peso é uma grandeza vetorial, medida em newtons.
e) Massa é uma grandeza escalar medida em quilogramas.
Gabarito: Letra C
Resolução:
A única afirmativa incorreta é a letra C, nela é dito que o peso aponta para baixo, o que está errado. Uma vez que a força peso é uma grandeza vetorial, sua definição depende de um referencial. Para nós, por exemplo, uma pessoa em outro lado do globo tem o seu peso apontando para cima. O correto seria dizer que o peso aponta sempre para o centro da Terra.
Questão 2) Na Lua, onde a gravidade é igual a 1,6 m/s², o peso de uma pessoa é de 80 N. Na Terra, onde a gravidade é de 9,8 m/s², a massa dessa pessoa, em kg, será igual a:
a) 490,0 kg
b) 50,0 kg
c) 8,2 kg
d) 784,0 kg
e) 128 kg
Gabarito: Letra B
Resolução:
Primeiramente devemos calcular a massa da pessoa com base em seu peso e na gravidade na Lua, confira:
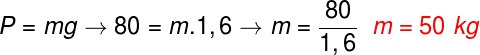
Pelos cálculos anteriores, encontramos que a massa desse corpo é igual a 50 kg, no entanto, pede-se a massa do corpo na Terra, que deve ser igual à sua massa em qualquer outro lugar. Desse modo, a alternativa correta é a letra B.
Questão 3) Um objeto tem peso igual a 2231 N na superfície de Júpiter, onde a gravidade é de 24,79 m/s². Qual deve ser o peso desse corpo em Marte, onde a gravidade é de 3,7 m/s²?
a) 333 N
b) 90 N
c) 900 N
d) 370 N
e) 221 N
Gabarito: Letra A
Resolução:
Baseados na massa e no peso do corpo em Júpiter, podemos calcular sua massa em Marte, confira:
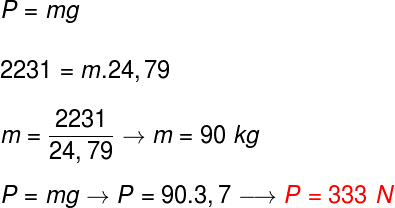
Depois de termos descoberto a massa do corpo (90 kg), aplicamos novamente a fórmula do peso, dessa vez utilizando a gravidade de Marte (3,7 m/s²). Desse modo, encontramos que o peso desse corpo em Marte deve ser de 333 N.
Por Me. Rafael Helerbrock
