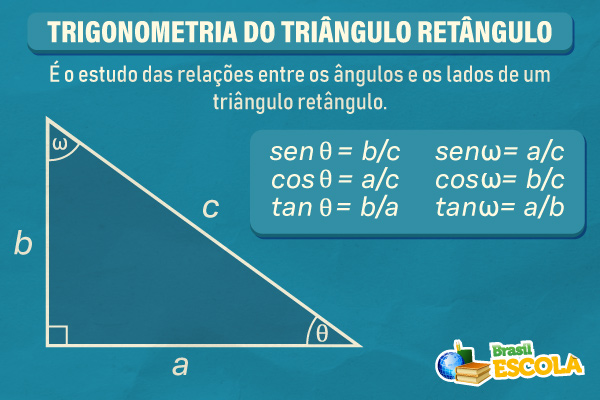
A trigonometria no triângulo retângulo é a área da Matemática que analisa a relação existente entre os ângulos de um triângulo e a medida dos seus lados. Ela é fundamental para diversas aplicações práticas, como na Engenharia, na Física, entre outras áreas. Os lados do triângulo retângulo recebem nomes especiais em relação ao ângulo, são eles: hipotenusa, cateto adjacente e cateto oposto.
As principais razões trigonométricas são seno, cosseno e tangente. Essas razões são a divisão entre dois lados do triângulo retângulo. Existem os ângulos notáveis, os que mais aparecem em problemas matemáticos e que medem 30º, 45º e 60º. Aprender o valor do seno, do cosseno e da tangente dos ângulos notáveis é fundamental para resolver situações envolvendo trigonometria.
Leia também: Teorema de Pitágoras — relação entre as medidas dos lados de um triângulo retângulo
Tópicos deste artigo
- 1 - Resumo sobre trigonometria no triângulo retângulo
- 2 - O que é a trigonometria do triângulo retângulo?
- 3 - Composição do triângulo retângulo
- 4 - Fórmulas da trigonometria do triângulo retângulo
- 5 - Relações trigonométricas do triângulo retângulo
- 6 - Ângulos notáveis
- 7 - Aplicações da trigonometria no triângulo
- 8 - Exercícios resolvidos sobre trigonometria do triângulo retângulo
Resumo sobre trigonometria no triângulo retângulo
- A trigonometria no triângulo retângulo é a área que analisa a relação entre a medida dos lados e dos ângulos do triângulo.
- Os lados do triângulo retângulo, a depender do ângulo a ser analisado, são conhecidos como hipotenusa, cateto oposto e cateto adjacente.
- As relações trigonométricas são seno, cosseno e tangente.
\(sen\alpha = \frac{\text{cateto oposto}}{\text{hipotenusa}}\)
\(cos\alpha = \frac{\text{cateto adjacente}}{\text{hipotenusa}}\)
\(tg\alpha = \frac{\text{cateto oposto}}{\text{cateto adjacente}}\)
- Os ângulos notáveis são os ângulos de 30º, 45º e 60º, e os valores do seno, cosseno e tangente desses ângulos são utilizados para facilitar a resolução de situações problemas.
O que é a trigonometria do triângulo retângulo?
A trigonometria do triângulo retângulo é o estudo das relações entre os ângulos e os lados de um triângulo retângulo. Seu principal objetivo é encontrar medidas desconhecidas de lados ou ângulos utilizando razões trigonométricas. No estudo da trigonometria, é possível encontrar uma proporção entre as medidas dos lados e o ângulo do triângulo retângulo. Trata-se das razões trigonométricas, as principais são: o seno, o cosseno e a tangente.
Composição do triângulo retângulo
Os lados do triângulo retângulo recebem nomes especiais, o maior lado é conhecido como hipotenusa, sempre oposta ao ângulo de 90°. Já os outros dois lados são chamados de catetos.
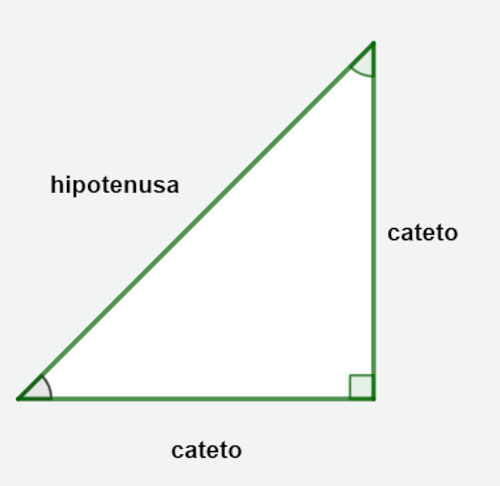
Agora, a depender do ângulo interno que estamos analisando, o cateto pode ser conhecido como cateto adjacente ou cateto oposto. Como o nome sugere, cateto oposto é o cateto que está oposto ao ângulo, já o cateto adjacente é o cateto que, como a hipotenusa, é um lado do ângulo. Veja a seguir:
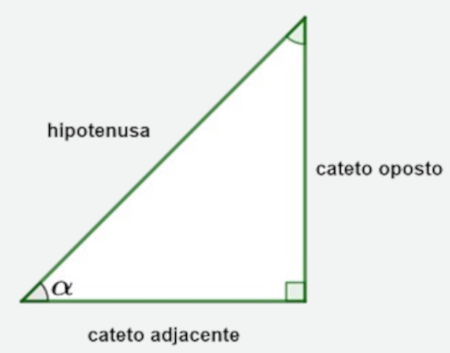
Cateto oposto e cateto adjacente considerando-se o ângulo α.
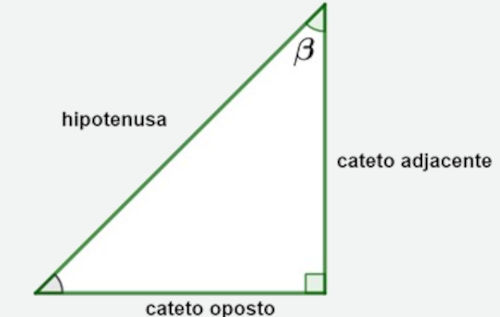
Cateto oposto e cateto adjacente considerando-se o ângulo β.
Fórmulas da trigonometria do triângulo retângulo
As principais razões trigonométricas são o seno, o cosseno e a tangente. As fórmulas de cada uma delas são:
- Fórmula do seno:
\(sen\alpha = \frac{\text{cateto oposto}}{\text{hipotenusa}}\)
- Fórmula do cosseno:
\(cos\alpha = \frac{\text{cateto adjacente}}{\text{hipotenusa}}\)
- Fórmula da tangente:
\(tan\alpha = \frac{\text{cateto oposto}}{\text{cateto adjacente}}\)
Veja também: Quais são as identidades trigonométricas?
Relações trigonométricas do triângulo retângulo
Além das fórmulas da trigonometria, existem as relações trigonométricas. As principais são:
\(sen^2\alpha + cos ^2\alpha = 1\)
\(1 + tan^2\alpha = \frac{1}{cos^2\alpha}\)
\(tan\alpha = \frac{sen\alpha}{cos \alpha}\)
Ângulos notáveis
Os ângulos notáveis — 30°, 45° e 60° — são amplamente utilizados em trigonometria porque têm razões trigonométricas exatas que facilitam cálculos. Os valores do seno do cosseno e da tangente dos ângulos notáveis são normalmente representados pela tabela a seguir:
|
|
30º |
45º |
60º |
|
sen |
\(\frac{1}{2}\) |
\(\frac{\sqrt 2}{2}\) |
\(\frac{\sqrt 3}{2}\) |
|
cos |
\(\frac{\sqrt 3}{2}\) | \(\frac{\sqrt 2}{2}\) | \(\frac{1}{2}\) |
|
tan |
\(\frac{\sqrt 3}{3}\) |
1 |
\({\sqrt 3}\) |
→ Videoaula sobre ângulos notáveis
Aplicações da trigonometria no triângulo
Agora que conhecemos as razões trigonométricas e os ângulos notáveis, vamos ver alguns exemplos de aplicação da trigonometria para encontrar valores desconhecidos em um triângulo retângulo.
- Exemplo 1:
Encontre o valor de x no triângulo retângulo a seguir:
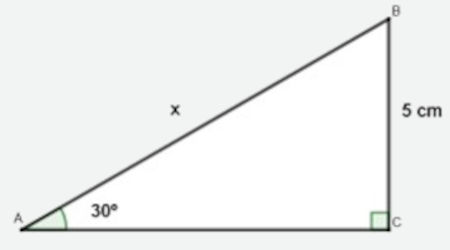
Resolução:
Analisando o ângulo conhecido, é possível identificar que x é a hipotenusa desse triângulo e que o lado cuja medida é igual a 5 cm é o cateto oposto ao ângulo.
A razão trigonométrica que relaciona cateto oposto e hipotenusa é o seno, pois sabemos que:
\(sen\alpha = \frac{\text{cateto oposto}}{\text{hipotenusa}}\)
Então temos que:
\(sen 30º = \frac{5}{x}\)
Consultando a tabela dos ângulos notáveis, sabemos que \(sen 30º = \frac{1}{2}\), então temos:
\(\frac{1}{2} = \frac{5}{x}\)
Multiplicando cruzado:
\(1x = 5\cdot 2\)
x = 10
Então x = 10 cm
- Exemplo 2:
Analisando a imagem a seguir, calcule o valor de x:
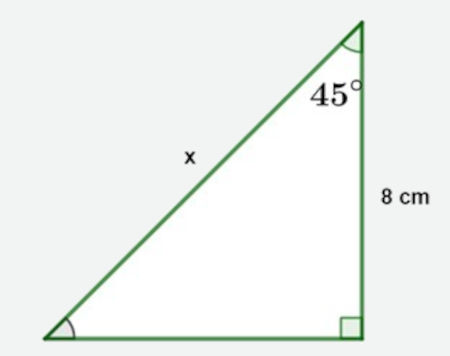
Resolução:
Analisando a imagem, é possível identificar que o lado que mede 8 cm corresponde ao cateto adjacente ao ângulo de 45º e que o lado que mede x corresponde à hipotenusa desse triângulo, então a razão trigonométrica que relaciona cateto adjacente e hipotenusa é o cosseno.
\(cos\alpha = \frac{\text{cateto adjacente}}{\text{hipotenusa}}\)
\(cos 45º = \frac{8}{x}\)
Ao consultar a tabela dos ângulos notáveis, temos que:
\(cos 45º = \frac{\sqrt 2}{2}\)
Logo, temos que:
\(\frac{\sqrt 2}{2} = \frac{8}{x}\)
\(x\sqrt 2 = 2\cdot 8\)
\(x\sqrt 2 = 16\)
\(x = \frac{16}{\sqrt 2}\)
Racionalizando:
\(x = \frac{16}{\sqrt 2} \cdot \frac{\sqrt 2}{\sqrt 2} \)
\(x = \frac{16\sqrt 2}{2}\)
\(x = 8\sqrt 2\)
- Exemplo 3:
Analisando o triângulo a seguir, calcule o valor de x:
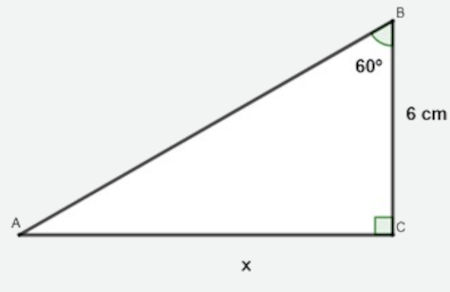
Resolução:
Analisando a imagem, é possível identificar que o lado que mede 6 cm corresponde ao cateto adjacente ao ângulo de 60º e que o lado que mede x corresponde ao cateto oposto desse triângulo, então a razão trigonométrica que relaciona cateto adjacente e cateto oposto é a tangente.
\(tan\alpha = \frac{\text{cateto oposto}}{\text{cateto adjacente}}\)
\(tan 60º = \frac{6}{x}\)
Consultando a tabela dos ângulos notáveis,\(tan 60º = {\sqrt 3}\).
\({\sqrt 3} = \frac{6}{x}\)
\(x{\sqrt 3} = 6\)
\(x = \frac{6}{\sqrt3}\)
Racionalizando:
\(x=\frac{6}{\sqrt 3} \cdot \frac{\sqrt 3}{\sqrt 3}\)
\(x=\frac{6\sqrt 3} {3}\)
\(x=2\sqrt 3\)
Saiba mais: Como é feita a classificação dos triângulos
Exercícios resolvidos sobre trigonometria do triângulo retângulo
Heitor quer instalar uma escada para acessar o telhado de sua casa. A escada forma um ângulo de 60° com o chão e seu comprimento é de 5 metros. Qual a altura aproximada do telhado, considerando que a escada toca a parede no ponto mais alto? (use √3 = 1,7)
A) 2,50 m
B) 4,25 m
C) 3,80 m
D) 5,00 m
E) 6,35 m
Resolução:
Alternativa B
A escada representa a hipotenusa do triângulo retângulo, e a altura do telhado é o cateto oposto ao ângulo de 60°. Utilizamos a relação:
\(sen 60º = \frac{h}{5}\)
Sabemos que \(sen 60º = \frac{\sqrt 3}{2}\)
\( \frac{\sqrt3}{2} = \frac{h}{5}\)
\(2h = 5\sqrt3\)
\(h= \frac{5\sqrt3}{2}\)
\(h= \frac{5\cdot 1,7}{2}\)
\(h=4,25\)
Questão 2
Uma árvore projetou uma sombra de 12 metros no chão. Se o ângulo de elevação do Sol em relação ao topo da árvore é de 30°, qual é a altura aproximada da árvore? (use √3 = 1,7)
A) 3,5 m
B) 6,8 m
C) 12,2 m
D) 18,0 m
E) 24,6 m
Resolução:
Alternativa B
Neste caso, a árvore representa o cateto oposto e a sombra é o cateto adjacente. Usamos a tangente:
\(\tan 30^\circ = \frac{h}{12}\)
Consultando a tabela, sabemos que:
\(\tan 30^\circ = \frac{\sqrt{3}}{3} \\\)
Logo:
\(\frac{h}{12} = \frac{\sqrt{3}}{3} \\ 3h = 12\sqrt{3} \\ h = \frac{12\sqrt{3}}{3} \\ h = 4\sqrt{3} \\ h = 4 \cdot 1,7 \\ h = 6,8\)
Questão 3
Um engenheiro precisa medir a altura de um poste. Ele se posiciona a 8 metros da base do poste e mede um ângulo de elevação de 45° até o topo. Qual é a altura do poste?
A) 4 m
B) 6 m
C) 8 m
D) 10 m
E) 12 m
Resolução:
Alternativa C
A relação trigonométrica que utilizamos aqui é a tangente, pois temos o cateto oposto, que é a altura do poste, e o cateto adjacente, que é a distância do engenheiro até a base do poste.
\(\tan 45^\circ = \frac{x}{8}\)
Ao consultar a tabela, temos que tan 45° = 1, logo:
\(1 = \frac{x}{8} \\ x = 8 \cdot 1 \\ x = 8\)
Fontes
DANTE, Luiz Roberto. Matemática: Contexto e Aplicações. 1. ed. São Paulo: Ática, 2005. 3 v.
MORGADO, Augusto César de Oliveira. Trigonometria e Números Complexos. 1. ed. Rio de Janeiro: Sociedade Brasileira de Matemática, 1999.