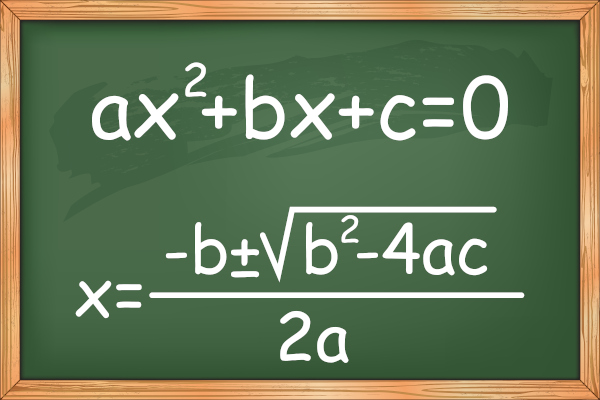Equação do 2º grau

A equação do 2º grau é caracterizada por um polinômio de grau 2, ou seja, um polinômio do tipo ax²+bx+c, em que a, b e c são números reais. Ao resolvermos uma equação de grau 2, estamos interessados em encontrar valores para a incógnita x que torne o valor da expressão igual a 0, que são chamadas de raízes, isto é, ax² + bx +c = 0.

Leia também: Diferenças entre função e equação

Tópicos deste artigo

• 1 - Tipos de equações do 2º grau
• 2 - Como resolver equações de 2º grau?
  • → Exemplo
  • Método de solução para equações do tipo ax²+ c = 0
  • → Exemplo
  • Método de solução para equações do tipo ax2 + bx = 0
  • → Exemplo
  • Método de solução para equações completas
  • → Exemplo
• 3 - Sistemas de equações do segundo grau
  • → Exemplo
  • → Exemplo
• 4 - Exercícios resolvidos

Tipos de equações do 2º grau

A equação de 2º grau pode ser representada por ax²+bx+c=0, em que os coeficientes a, b e c são números reais, com a ≠ 0.

→ Exemplos

a) 2x² +4x – 6 = 0 → a = 2; b =4 e c = – 6

b) x² – 5x + 2 = 0 → a =1; b= – 5 e c = 2

c) 0,5x² + x –1 = 0 → a = 0,5; b = 1 e c = –1

A equação do 2º grau é classificada como completa quando todos os coeficientes são diferentes de 0, ou seja, a ≠ 0, b ≠ 0 e c ≠ 0.

A equação do 2º grau é classificada como incompleta quando o valor dos coeficientes b ou c são iguais a 0, isto é, b = 0 ou c = 0.

→ Exemplos

a) 2x² – 4 = 0 → a = 2; b = 0 e c= – 4

b) -x² + 3x = 0 → a = – 1; b = 3 e c = 0

c) x² = 0 → a = 1; b =0 e c =0

Atenção: o valor do coeficiente a nunca é igual a 0, caso isso ocorra, a equação deixa de ser do 2º grau.

Como resolver equações de 2º grau?

A solução de uma equação do 2º grau ocorre, quando as raízes são encontradas, ou seja, os valores atribuídos a x . Esses valores de x devem tornar a igualdade verdadeira, isto é, ao substituir o valor de x na expressão, o resultado deve ser igual a 0.

→ Exemplo

Considerando a equação x² – 1 = 0 temos que x’ = 1 e x’’ = – 1 são soluções da equação, pois substituindo esses valores na expressão, temos uma igualdade verdadeira. Veja:

x² – 1 = 0

(1)² – 1 = 0 e (–1)² – 1 = 0

Para encontrar a solução de uma equação, é preciso analisar se a equação é completa e incompleta e selecionar qual método será utilizado.

• Método de solução para equações do tipo ax²+ c = 0

O método para determinar a solução de equações incompletas que possuem b=0 consiste em isolar a incógnita x, assim:

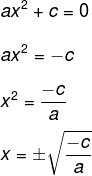
→ Exemplo

Encontre as raízes da equação 3x² – 27 = 0.

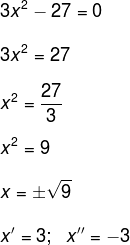
Se quiser saber mais sobre esse método, acesse: equação incompleta do 2º grau com coeficiente b nulo.

• Método de solução para equações do tipo ax² + bx = 0

O método para determinar as possíveis soluções de uma equação com c =0, consiste em utilizar a fatoração por evidência. Veja:

ax² + bx = 0

x·(ax + b) = 0

Ao observar a última igualdade, é notável que há uma multiplicação e que para o resultado ser 0, é necessário que, pelo menos, um dos fatores seja igual a 0.

x·(ax + b) = 0

x = 0 ou ax + b = 0

Assim, a solução da equação é dada por:

→ Exemplo

Determine a solução da equação 5x² – 45x = 0

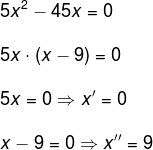
Se quiser saber mais sobre esse método, acesse: equação incompleta do 2º grau com coeficiente c nulo.

• Método de solução para equações completas

O método conhecido como método de Bhaskara ou fórmula de Bhaskara aponta que as raízes de uma equação do 2º grau do tipo ax² + bx + c = 0 é dada pela seguinte relação:

→ Exemplo

Determine a solução da equação x² – x – 12 = 0.

Note que os coeficientes da equação são: a = 1; b= – 1 e c = – 12. Substituindo esses valores na fórmula de Bhaskara, temos:

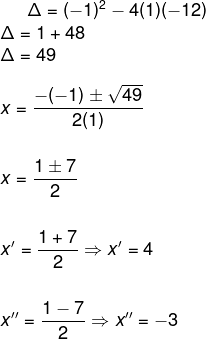
O delta (Δ) recebe o nome de discriminante e note que ele está dentro de uma raiz quadrada e, conforme sabemos, levando em conta os números reais, não é possível extrair raiz quadrada de um número negativo.

Conhecendo o valor do discriminante, podemos realizar algumas afirmações a respeito da solução da equação do 2º grau:

→ discriminante positivo (Δ > 0): duas soluções para a equação;

→ discriminante igual a zero (Δ = 0): as soluções da equação são repetidas;

→ discriminante negativo (Δ < 0): não admite solução real.

Sistemas de equações do segundo grau

Quando consideramos simultaneamente duas ou mais equações, temos um sistema de equações. A solução de um sistema de 2 variáveis é o conjunto de pares ordenados que satisfaz simultaneamente todas as equações envolvidas.

→ Exemplo

Considere o sistema:

Com os valores: x’ = 2, x’’ = – 2 e y’ = 2, y’’ = – 2 podemos montar pares ordenados que satisfazem as equações do sistema simultaneamente. Veja: (2, 2), (2, – 2), (– 2, 2), (– 2, – 2).

Lembre-se de que um par ordenado é escrito da forma (x, y).

Os métodos para encontrar a solução de um sistema de equações são semelhantes ao de sistemas lineares.

→ Exemplo

Considere o sistema:

Da equação x – y = 0, vamos isolar a incógnita x, assim:

x – y = 0

x = y

Agora devemos substituir o valor isolado na outra equação, assim:

x² – x –12 = 0

y² – y –12 = 0

Utilizando método de Bhaskara, temos que:

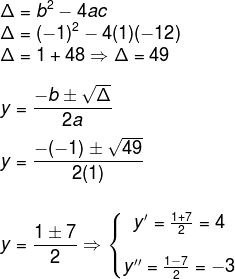
Como x = y, teremos que x’ = y’ e x’’ = y’’. Ou seja:

x’ = 4

x’’ = -3

Assim, os pares ordenados são soluções do sistema (4, 4) e (– 3,– 3).

Leia mais: Sistema de equações do 1º e 2º grau

Exercícios resolvidos

Questão 1 – (ESPM -SP) As soluções da equação abaixo são dois números

a) primos.

b) positivos.

c) negativos.

d) pares.

e) ímpares.

Solução

Sabemos que os denominadores de uma fração não podem ser iguais a zero, logo x ≠1 e x≠3. E como temos uma igualdade de frações, podemos realizar a multiplicação cruzada, obtendo:

(x+3) · (x+3) = (x – 1) · (3x +1)

x² + 6x +9 = 3x² – 2x – 1

x² – 3x² + 6x + 2x +9 +1 = 0

(– 1) – 2x² + 8x +10 = 0 (– 1)

2x² – 8x – 10 = 0

Dividindo por 2 ambos os lados da equação, temos:

x² – 4x – 5 = 0

Utilizando a fórmula de Bhaskara segue que:

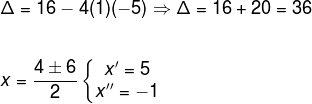
Observe que as raízes da equação são números ímpares.

Alternativa e.

Questão 2 – (UFPI) Um criador de aves verificou que, após colocar (n +2) aves em cada um dos n viveiros disponíveis, sobraria apenas uma ave. O número total de aves, para qualquer valor de n natural, é sempre

a) um número par.

b) um número ímpar.

c) um quadrado perfeito.

d) um número divisível por 3.

e) um número primo.

Solução

A quantidade de aves pode ser encontrada multiplicando o número de viveiros pela quantidade de aves colocada em cada um deles, pelo enunciado do exercício depois de fazer esse processo ainda sobra uma ave, podemos escrever tudo isso da seguinte maneira:

n·(n+2) +1

Realizando a distributividade vamos obter:

n² + 2n +1

E fatorando esse polinômio segue que:

(n +1)²

Assim, o número toral de aves é sempre um quadrado perfeito para qualquer número natural n.

Alternativa C

 

Por Robson Luiz
Professor de Matemática