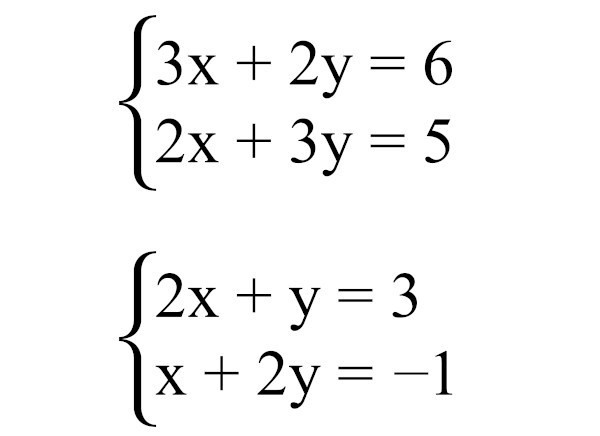Sistemas lineares

Resolver sistemas lineares é uma tarefa bastante recorrente para estudos nas áreas das ciências da natureza e da matemática. A busca por valores desconhecidos fez com que fossem desenvolvidos métodos de resolução de sistemas lineares, como o método da adição, igualdade e substituição para sistemas que possuem duas equações e duas incógnitas, e a regra de Crammer e o escalonamento, que resolvem sistemas lineares de duas equações, mas que são mais convenientes para sistemas  com mais equações. Um sistema linear é um conjunto de duas ou mais equações com uma ou mais incógnitas.

Leia também: Qual a relação entre matrizes e sistemas lineares?

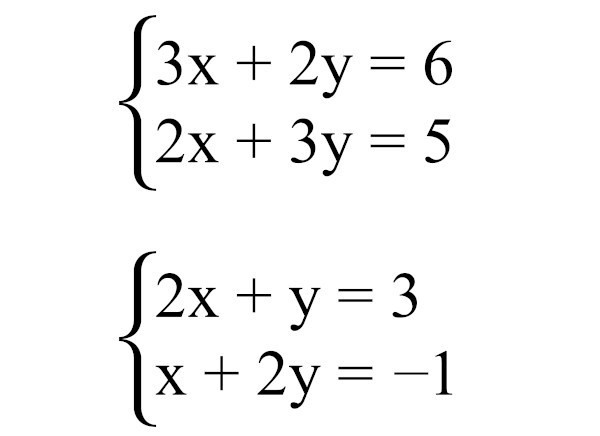
Tópicos deste artigo

• 1 - Equação linear
• 2 - Resolução de sistemas lineares
  • Sistemas lineares com duas equações do 1º grau e duas incógnitas
  • Método da adição
  • Sistemas lineares com três equações do 1º grau e três incógnitas
• 3 - Classificação de sistema linear
• 4 - Exercícios resolvidos

Equação linear

O trabalho com equações existe devido à necessidade de encontrarmos valores desconhecidos de incógnitas. Chamamos de equação quando temos uma expressão algébrica com igualdade, e ela é classificada como linear quando o maior expoente de suas incógnitas é 1, conforme os exemplos a seguir:

2x + y = 7 → equação linear com duas incógnitas

a + 4 = -3 → equação linear com uma incógnita

De modo geral, uma equação linear pode ser descrita por:

a₁x₁ + a₂x₂ + a3x3… + a_nx_n = c

Conhecemos como sistema de equação quando há mais de uma equação linear. Começaremos com sistemas lineares de duas incógnitas.

Resolução de sistemas lineares

• Sistemas lineares com duas equações do 1º grau e duas incógnitas

Para resolver um sistema de duas equações e duas incógnitas, existem vários métodos, os três mais conhecidos são:

• método da comparação
• método da adição
• método da substituição

Qualquer um dos três pode resolver um sistema linear de duas equações e duas incógnitas. Esses métodos não são tão eficientes para sistemas com mais equações, já que existem outros métodos específicos para resolvê-los.

• Método da substituição

O método da substituição consiste em isolar uma das incógnitas em uma das equações e realizar a substituição na outra equação.

Exemplo:

1º passo: isolar uma das incógnitas.

Chamamos de I a primeira equação e de II a segunda equação. Analisando as duas, vamos escolher a incógnita que esteja mais fácil de ser isolada. Note que, na equação I → x + 2y = 5, o x não possui coeficiente, o que faz com que seja mais fácil isolá-lo, logo, reescreveremos a equação I desta forma:

I → x + 2y = 5

I → x = 5 – 2y

2º passo: substituir I em II.

Agora que temos a equação I com o x isolado, na equação II, podemos substituir x por 5 – 2y.

II → 3x – 5y = 4

Substituindo x por 5 – 2y:

3 (5 – 2y) – 5y = 4

Agora que a equação tem só uma incógnita, é possível resolvê-la para encontrar o valor de y.

Conhecendo o valor de y, encontraremos o valor de x realizando a substituição do valor de y na equação I.

I → x = 5 – 2y

x = 5 – 2 · 1

x = 5 – 2

x = 3

Então a solução do sistema é S = {3,1}.

• Método da comparação

O método da comparação consiste em isolarmos uma incógnita nas duas equações e igualar esses valores.

Exemplo:

1º passo: seja I a primeira equação e II a segunda, vamos isolar uma das incógnitas em I e II. Escolhendo isolar a incógnita x, temos que:

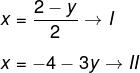
2º passo: igualar as duas novas equações, já que x = x.

3º passo: substituir o valor de y por -2 em uma das equações.

x = -4 – 3y

x = -4 – 3 (-2)

x = -4 + 6

x = 2

Então a solução desse sistema é o conjunto S = {2,-2}.

Veja também: Quais as diferenças entre função e equação?

• Método da adição

O método da adição consiste em realizar a multiplicação de todos os termos de uma das equações, de tal modo que, ao somar-se a equação I na equação II, uma de suas incógnitas fique igual a zero.      

Exemplo:

1º passo: multiplicar uma das equações para que os coeficientes fiquem opostos.

Note que, se multiplicarmos a equação II por 2, teremos 4y na equação II e -4y na equação I, e que, ao somarmos I + II, teremos 0y, logo, vamos multiplicar todos os termos da equação II por 2 para que isso aconteça.

I → 5x – 4y = -5

2 · II → 2x + 4y = 26

2º passo: realizar a soma I + 2 · II.

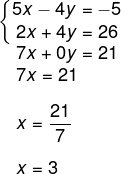
3º passo: substituir o valor de x = 3 em uma das equações.

 

 

 

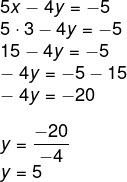
• Sistemas lineares com três equações do 1º grau e três incógnitas

Quando o sistema possui três incógnitas, adotamos outros métodos de resolução. Todos esses métodos relacionam os coeficientes com matrizes, e os métodos mais utilizados são a regra de Crammer ou o escalonamento. Para a resolução em ambos os métodos, é necessário a representação matricial do sistema, inclusive o sistema 2x2 pode ser representado por meio de uma matriz. Há duas possíveis representações, a matriz completa e a matriz incompleta:

Exemplo:

O sistema 

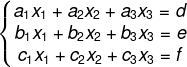
Pode ser representado pela matriz completa

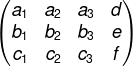
E pela matriz incompleta

• Regra de Crammer

Para encontrarmos soluções de um sistema 3x3, com incógnitas x, y e z, utilizando a regra de Crammer, é necessário calcularmos o determinante da matriz incompleta e suas variações. Temos então que:

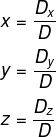
D → determinante da matriz incompleta do sistema.

D_x → determinante da matriz incompleta do sistema, substituindo-se a coluna de x pela coluna dos termos independentes.

D_y → determinante da matriz incompleta do sistema, substituindo-se a coluna de y pela coluna dos termos independentes.

D_z → determinante da matriz incompleta do sistema, substituindo-se a coluna de z pela coluna dos termos independentes.

Dessa forma, para encontrar o valor de suas incógnitas, primeiro precisamos calcular o determinante D, D_x, D_y associado ao sistema.

Exemplo:

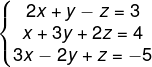
1º passo: calcular D.

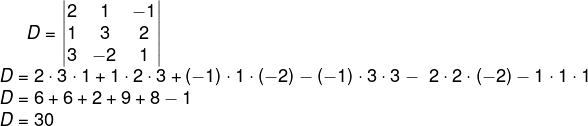
2º passo: calcular D_x.

3º passo: então podemos encontrar o valor do x, pois:

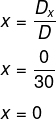
4º passo: calcular D_y.

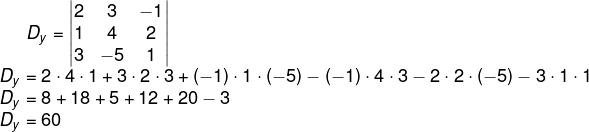
5º passo: então podemos calcular o valor de y:

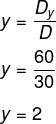
6º passo: agora que conhecemos o valor de x e y, em qualquer uma das linhas podemos encontrar o valor de z substituindo o valor de x e y e isolando o z. Outra opção é calcular D_z.

Substituindo x = 0 e y = 2 na primeira equação:

2x + y – z = 3

2 · 0 + 2 – z = 3

0 + 2 – z = 3

-z = 3 – 2

-z = -1 (-1)

 z = -1

Portanto, a solução do sistema é a terna (0,2,-1).

Acesse também: Resolução de problemas por sistemas de equação  

• Escalonamento

Outro método de resolver sistemas lineares é o escalonamento, nele utilizamos somente a matriz completa e operações entre as linhas com o objetivo de isolar as suas incógnitas. Vamos escalonar o sistema a seguir.

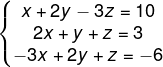
1º passo: escrever a matriz completa que represente o sistema.

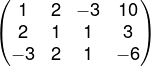
Seja L₁, L₂ e L₃ respectivamente as linhas 1, 2 e 3 da matriz, vamos realizar operações entre L₁ e L₂ e  L₁ e L₃, de modo que o resultado faça com que os termos que estão na primeira coluna da segunda e da terceira linhas fiquem iguais a zero.

Analisando a segunda linha da matriz, vamos substituí-la pelo resultado de L2 → -2 · L1 + L2, com objetivo de zerar o termo a21.

a₂₁ = -2 · 1 + 2 = 0

a₂₂ =  -2 · 2 + 1 = -3  

a₂₃ = -2 · (-3) + 1 = 7

a₂₄ =  -2 · 10 + 3 = -17

Então a L₂ será 0  -3  7  -17.

Analisando a terceira linha da matriz, vamos substituí-la pelo resultado de L3 → 3L1 + L_2, com o objetivo de zerar o termo a_31.

a₃₁ = 3 · 1 – 3 = 0

a₃₂ = 3 · 2 + 2 = 8

a₃₃ = 3 · (-3) +1 = -8

a₃₄ = 3 · 10 – 6 = 24

Então a L₃ será  0  8  -8  24. 

Note que todos são divisíveis por 8, logo, para que a linha L₃ fique mais simplificada, vamos dividi-la por 8.

L₃ → L₃ : 8 será: 0  1  -1  3.

Assim a nova matriz da equação escalonada será:

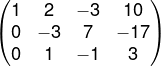
Agora o objetivo é zerar a coluna y na terceira linha, realizaremos operações entre a L₂ e L₃, com o objetivo de zerar a segunda coluna de uma delas.

Substituiremos a L3 por L3 → L₂ + 3L₃.

a₃₁ = 0 + 3 · 0 = 0

a₃₂ = -3 + 3 · 1 = 0

a₃₃ = 7 + 3 · (-1) = 4

a₃₄ = -17 + 3 · 3 = -8

Então L₃ será: 0  0  4  -8.

A nova matriz escalonada será:

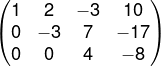
Agora, ao representarmos essa matriz como um sistema novamente, adicionando x, y e z nas colunas, encontraremos o seguinte:

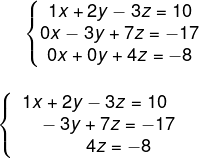
Podemos então encontrar o valor de cada uma das incógnitas. Analisando a equação III, temos que:

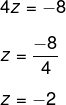
Se z = -2, vamos substituir o valor de z na segunda equação:

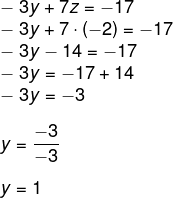
Por fim, na primeira equação, vamos substituir o valor de y e z para encontrarmos o valor de x.

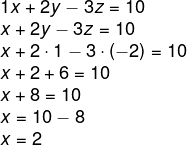
Veja também: Sistema de inequações de 1º grau – como resolver?

Classificação de sistema linear

Um sistema linear é um conjunto de equações lineares, podendo ter várias incógnitas e várias equações. Existem vários métodos para resolvê-lo, independentemente da quantidade de equações. Existem três classificações para um sistema linear.

• Sistema possível determinado (SPD): quando possui uma única solução.
• Sistema possível indeterminado (SPI): quando possui infinitas soluções.
• Sistema impossível (SI): quando não existe nenhuma solução.

Exercícios resolvidos

Questão 1 (IFG 2019) Considere a soma das medidas de uma base e da altura relativa a essa base de um triângulo igual a 168 cm e a diferença igual a 24 cm. É correto afirmar que as medidas da base e da altura relativa a essa base medem, respectivamente:

a) 72 cm e 96 cm

b) 144 cm e 24 cm

c) 96 cm e 72 cm

d) 24 cm e 144 cm

Resolução

Alternativa C.

Seja h → altura e b → base, então temos o seguinte sistema:

Pelo método da adição, temos que:

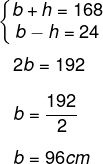
Para encontrar o valor de h, vamos substituir b = 96 cm na primeira equação:

b + h = 168

96 + h = 168

h = 168 – 96

h = 72 cm

Questão 2 A matriz incompleta que representa o sistema linear a seguir é:

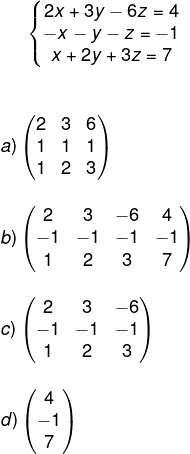
Resolução

Alternativa C.

A matriz incompleta é aquela que possui os coeficientes de x, y e z, logo, ela será uma matriz 3x3. Analisando-se as alternativas, a que contém a matriz 3x3 com os sinais corretos é a de letra C.

 

Por Raul Rodrigues de Oliveira
Professor de Matemática