O que são quadriláteros?

Quadriláteros são polígonos que possuem quatro lados. Os polígonos, por sua vez, são figuras limitadas por segmentos de reta. Sendo assim, todos os lados de um polígono e, por consequência, de um quadrilátero são retos.

Elementos de um quadrilátero

Lados: São os segmentos de reta que contornam o quadrilátero;

• Vértices: São os pontos de encontro entre dois lados;

• Ângulos internos: São os ângulos determinados por dois lados consecutivos de um quadrilátero;

• Ângulos externos: são ângulos formados pelo prolongamento de um lado de um polígono. Um ângulo externo sempre é suplementar ao ângulo interno adjacente a ele;

• Diagonais: Segmentos de reta cujas extremidades são dois vértices não consecutivos de um polígono. Dessa maneira, são os segmentos de reta que ligam dois vértices e que, ao mesmo tempo, não são lados.

Propriedades gerais dos quadriláteros

• A soma dos ângulos internos de um quadrilátero é sempre igual a 360°;

• A soma entre um ângulo interno de um quadrilátero e o ângulo externo adjacente a ele é igual a 180°;

• O perímetro de um quadrilátero é igual à soma dos comprimentos de seus lados.

Quadriláteros convexos ou não convexos

Convexo é o nome dado a um polígono que possui a seguinte característica: a reta que contém um de seus lados não corta o polígono, qualquer que seja o lado escolhido para observar essa reta.

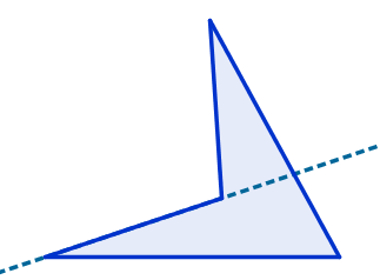
Em outras palavras, um polígono convexo não possui vértices voltados para dentro, formando uma espécie de boca. Observe a imagem com um exemplo de quadrilátero não convexo, em que a reta que contém um lado corta o polígono:

Trapézios

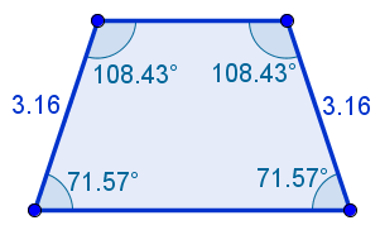
Trapézios são quadriláteros que possuem um par de lados opostos e paralelos. Todas as características e propriedades dos quadriláteros e dos polígonos valem para os trapézios. Além dessas, também é possível que os trapézios possuam uma característica específica, o que lhes garante também uma propriedade específica.

Um trapézio é chamado de isósceles quando os seus dois lados não paralelos (e opostos) são congruentes. Nesse caso, a propriedade específica é: em trapézios isósceles, os ângulos da base são congruentes.

Paralelogramos

Os paralelogramos são os quadriláteros que possuem dois pares de lados paralelos. Além de todas as propriedades e características dos polígonos, também possuem as seguintes propriedades específicas:

• Lados opostos são paralelos e congruentes;

• Ângulos opostos são congruentes;

• Ângulos internos adjacentes são suplementares;

• As diagonais de um paralelogramo encontram-se em seus pontos médios.

Os paralelogramos são comumente divididos em quatro grupos: paralelogramos quaisquer, retângulos, losangos e quadrados. O primeiro grupo é composto por paralelogramos que não pertencem aos outros três.

Retângulos

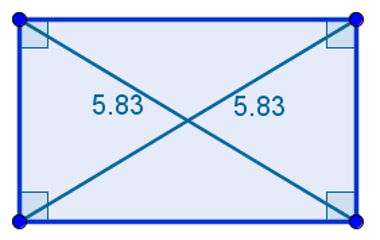
São paralelogramos que possuem todos os ângulos retos. Sendo assim, todos os seus ângulos são iguais a 90°. A propriedade específica dos retângulos é a seguinte:

“As diagonais de um retângulo são congruentes.”

Losangos

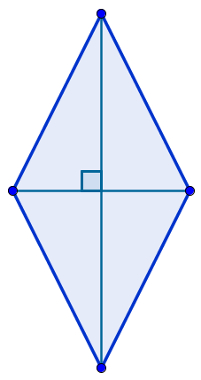
São paralelogramos que possuem todos os quatro lados congruentes. Observe que os losangos não precisam ter ângulos congruentes, com exceção dos ângulos opostos, é claro. A propriedade específica dos losangos é a seguinte:

“As diagonais de um losango são perpendiculares.”

Quadrados

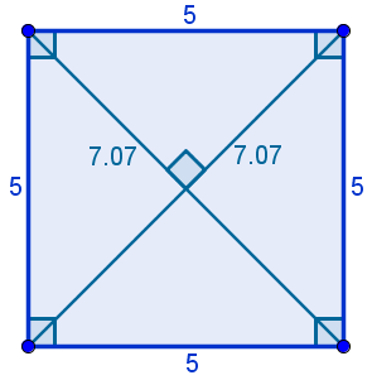
Os quadrados são losangos e retângulos ao mesmo tempo, ou seja, são paralelogramos que possuem todos os lados congruentes e todos os ângulos retos. Sendo assim, podemos afirmar que todo quadrado também é retângulo e losango, mas nem todo losango ou retângulo é quadrado.

A propriedade específica dos quadrados é a junção entre as propriedades do losango e do retângulo. Observe:

“As diagonais de um quadrado são perpendiculares e congruentes.”

Por Luiz Paulo Moreira
Graduado em Matemática