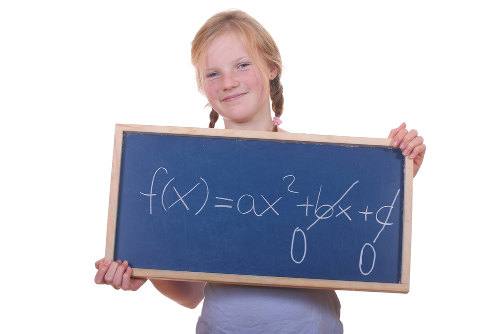O que são equações incompletas do segundo grau?

Uma equação do segundo grau é uma equação que pode ser escrita na forma ax² + bx + c = 0. As letras a, b e c representam números reais constantes chamados coeficientes, e o coeficiente a nunca pode ser igual a zero. Quando um dos outros dois coeficientes, ou ambos, é igual a zero, a equação do segundo grau formada é chamada de incompleta.

Assim, as equações incompletas podem ter uma das três formas a seguir:

ax² = 0

ax² + bx = 0

ax² + c = 0

Cada uma dessas equações pode ser resolvida por técnicas diferentes da fórmula de Bháskara ou pelo método de completar quadrados, que são exclusivos de cada uma das três formas.

Fórmula de Bháskara

Essa é, sem dúvidas, a fórmula mais conhecida para resolver equações do segundo grau e pode ser usada em qualquer equação. Desde que possua soluções reais, as raízes reais da equação serão obtidas por meio desse método, independentemente de a equação ser completa ou incompleta. Na realidade, essa fórmula pode ser usada até para encontrar soluções de equações que não possuem raízes reais, no conjunto dos números complexos.

A fórmula de Bháskara geralmente é apresentada em dois passos. Assim, o primeiro é o discriminante:

Δ = b² – 4ac

E o segundo é:

x = – b ± √?
       2a

Quando os coeficientes B e C são iguais a zero, teremos:

x = – b ± √(b² – 4ac)
              2a      

x = – 0 ± √(0² – 4a?·0)
              2a      

x =   0  
      2a

x = 0

Portanto, todas as vezes que os coeficientes B e C forem iguais a zero, teremos discriminante igual a zero e, por isso, a equação terá apenas uma raiz real. Nesse caso específico, esse resultado será zero, como encontramos no cálculo anterior.

Quando apenas o coeficiente C = 0, teremos:

x = – b ± √(b² – 4ac)
               2a         

x = – b ± √(b² – 4a?·0)
              2a      

x = – b ± √(b²)
          2a     

= – b ± b
       2a 

Isso resultará em x = 0 ou x = b/a.

Quando apenas o coeficiente B = 0, teremos uma equação com duas raízes reais e distintas.

Técnicas alternativas para cada tipo de equação

As técnicas apresentadas a seguir, na verdade, são apenas uma alternativa que foge ao uso da fórmula de Bháskara quando as equações são incompletas. Todos esses cálculos são baseados na simples solução de equações e nas propriedades das operações matemáticas.

Quando B e C são iguais a zero

Basta dividir toda a equação pelo valor do coeficiente a e fazer a raiz quadrada em ambos os membros da equação. Observe que o resultado sempre será zero, pois sempre teremos 0/a no segundo membro.

ax² = 0

ax² = 0
 a      a

x² = 0
       a

√x² = √(0/a)

x = ± 0 = 0

Quando B = 0

Se B for igual a zero, o procedimento é igual ao anterior, entretanto, deveremos “passar” o termo c/a para o segundo membro antes de fazer a raiz quadrada em ambos os membros. Observe que – c/a pode ser um número positivo, bastando, para isso, que a ou c seja um número negativo.

ax² + c= 0

ax² + c = 0
 a       a    a

ax² = – c
a         a

x² = – c/a

√x² = ± √(– c/a)

Exemplo:

2x² – 50 = 0

2x² = 50

x² = 25

√x² = √25

x = ± 5

Quando C = 0

Se C = 0, poderemos colocar x em evidência:

ax² + bx = 0

x(ax + b) = 0

Como isso é um produto, um dos fatores tem que ser zero para que a equação seja igual a zero. Portanto, x = 0 ou:

ax + b = 0

ax = – b

x = – b  
        a 

Exemplo:

3x² + 36 = 0

x(3x + 36) = 0

x = 0 ou

3x + 36 = 0

3x = – 36

x = – 36  
        3 

x = – 12

Logo, 0 e – 12 são as raízes.

Por Luiz Paulo Moreira
Graduado em Matemática