Uma equação do 2° grau é toda e qualquer equação com uma incógnita que é expressa da seguinte forma:
ax2 + bx + c = 0, a ≠ 0
A letra x é a incógnita, e as letras a, b e c são números reais que exercem a função de coeficientes da equação. Apenas o coeficiente a deve ser diferente de zero. Se nenhum dos coeficientes for nulo, dizemos que se trata de uma equação completa; mas se algum dos coeficientes b e c for zero, dizemos que é uma equação incompleta.
Quando resolvemos uma equação do 2° grau, podemos encontrar até dois resultados. Esses valores são chamados de raízes da equação. Veremos neste artigo como determinar as raízes de uma equação do 2° grau.
Seja a equação do 2° grau completa ou incompleta, podemos utilizar a Fórmula de Bhaskara para encontrar suas raízes. A fórmula de Bhaskara apresenta-se da seguinte forma:
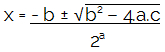
Apenas para simplificar a notação, comumente chamamos a expressão dentro da raiz quadrada de delta (?). Calculando o ? separadamente, nós podemos escrever a fórmula de Bhaskara da seguinte forma:
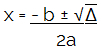
Caso o valor de delta seja menor que zero, dizemos que a equação do 2° grau não possui raízes reais. Se o delta for igual a zero, a equação terá duas raízes idênticas. Caso o delta seja maior que zero, a equação do 2° grau terá duas raízes distintas.
Vamos ver um exemplo de resolução de uma equação do 2° grau através da fórmula de Bhaskara.
x² + 3x + 2 = 0
Os coeficientes dessa equação são: a = 1, b = 3 e c = 2. Vamos calcular primeiramente o valor de delta:
? = b² – 4.a.c
? = 3² – 4.1.2
? = 9 – 8
? = 1
Agora que encontramos o valor de delta, vamos substituí-lo na Fórmula de Bhaskara para determinar as raízes de x:
x = – b ± √?
2.a
x = – 3 ± √1
2.1
x = – 3 ± 1
2
O sinal de ± resulta em duas raízes da equação. Dessa forma, primeiro encontraremos x', através do sinal +, e, em seguida, encontraremos x'', através do sinal de –:
x' = – 3 + 1
2
x' = – 2
2
x' = – 1
x'' = – 3 – 1
2
x'' = – 4
2
x'' = – 2
As raízes da equação x² + 3x + 2 = 0 são – 1 e – 2.
Caso a equação do 2° grau seja incompleta, podemos resolvê-la sem utilizar a fórmula de Bhaskara através dos princípios básicos da resolução de equações.
Por Amanda Gonçalves
Graduada em Matemática