PUBLICIDADE
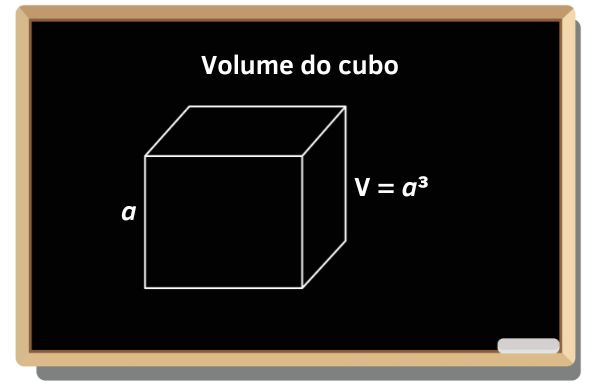
O volume do cubo é o espaço que esse sólido geométrico ocupa. O cubo, conhecido também como hexaedro, é o sólido geométrico composto por 6 faces quadradas. Logo, o volume do cubo depende somente da medida da sua aresta. O volume do cubo é igual ao comprimento da aresta elevado a 3, ou seja, V = a³.
Veja também: Volume do cilindro — como calcular?
Tópicos deste artigo
- 1 - Qual é a fórmula do volume do cubo?
- 2 - Como calcular o volume do cubo?
- 3 - Unidades de medida de volume
- 4 - Exercícios resolvidos sobre volume do cubo
Qual é a fórmula do volume do cubo?
Para entender a fórmula do volume do cubo, lembraremos as suas principais características. O cubo é um caso particular de poliedro. Ele é formado por 6 faces quadradas, 12 arestas e 8 vértices. No cubo, todas as arestas são congruentes. Além de poliedro, o cubo é considerado um paralelepípedo, já que todas as suas faces são formadas por quadrados. Observe a imagem a seguir.
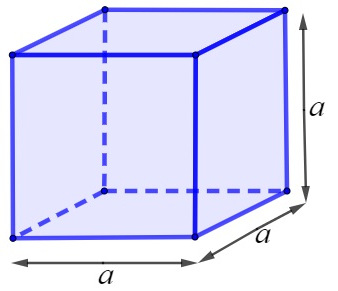
O volume do cubo é a multiplicação do comprimento pela altura e pela largura. Como todas as suas arestas são congruentes, medindo a, o volume do cubo nada mais é que o cubo da aresta, ou seja:
\(V=a^3\)
Como calcular o volume do cubo?
Para calcular o volume do cubo, conhecendo o comprimento da sua aresta, basta calcular o cubo da aresta.
-
Exemplo:
Um recipiente possui formato de um cubo com 12 centímetros de aresta, então o volume do cubo é de:
Resolução:
V = a³
V = 12³
V = 1728 cm³
O volume desse recipiente é de 1728 cm³.
-
Exemplo 2
Um poliedro possui 6 faces, todas quadradas, com arestas medindo 4 metros, então o volume desse poliedro é de:
Resolução:
Podemos perceber que esse poliedro é um cubo, logo basta calcular o volume do cubo:
V = a³
V = 4³
V = 64 m³
Leia também: Volume do cone — como calcular?
Unidades de medida de volume
Volume é o espaço que um determinado corpo ocupa e possui como unidade fundamental os metros cúbicos (m³). Além dos metros cúbicos, há os submúltiplos e os múltiplos dessa unidade de medida.
Os submúltiplos são:
-
milímetro cúbico: mm³
-
centímetro cúbico: cm³
-
decímetro cúbico: dm³
Os múltiplos são:
-
decâmetro cúbico: dam³
-
hectômetro cúbico: hm³
-
quilômetro cúbico: km³
Podemos também relacionar a medida de volume com a medida de capacidade, que é medida em litros. De modo geral, temos que:
1 m³ = 1000 l
1 dm³ = 1 l
1 cm³ = 1 ml
Exercícios resolvidos sobre volume do cubo
Questão 1
(Enem 2010) Um porta-lápis de madeira foi construído no formato cúbico, seguindo o modelo ilustrado a seguir. O cubo de dentro é vazio. A aresta do cubo maior mede 12 cm, e a do cubo menor, que é interno, mede 8 cm.
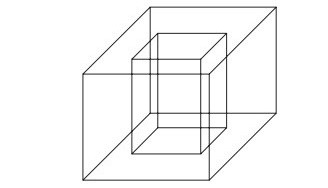
O volume de madeira utilizado na confecção desse objeto foi de
A) 12 cm³
B) 64 cm³
C) 96 cm³
D) 1216 cm³
E) 1728 cm³
Resolução:
Alternativa D
Para calcular o volume de madeira, calcularemos a diferença entre o volume do cubo maior e o volume do cubo menor.
O cubo menor possui aresta medindo 8 cm:
\(V_1=8^3\)
\(V_1=512\)
O cubo maior possui aresta medindo 12 cm:
\(V_2={12}^3\)
\(V_2=1728\)
Calculando a diferença entre eles, conclui-se que o volume de madeira usado foi de:
\(V=V_2-V_1\)
\(V=1728-512\)
\(V=1216\ cm^3\)
Questão 2
(Vunesp 2011) Os produtos de uma empresa são embalados em caixas cúbicas, com 20 cm de aresta. Para transporte, essas embalagens são agrupadas, formando um bloco retangular, conforme mostrado na figura. Sabe-se que 60 desses blocos preenchem totalmente o compartimento de carga do veículo utilizado para o seu transporte.
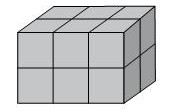
Pode-se concluir, então, que o volume máximo, em metros cúbicos, transportado por esse veículo é:
A) 4,96.
B) 5,76.
C) 7,25.
D) 8,76.
E) 9,60.
Resolução:
Alternativa B
Primeiramente, calcularemos o volume de um cubo. Sabendo que a sua aresta tem 20 cm e transformando esse valor em metros, temos 0,2 m de aresta.
\(V_{cubo}={0,2}^3\)
\(V_{cubo}=0,008\ m^3\)
Pela imagem é possível perceber que cada bloco retangular possui 12 cubos, então o volume do bloco será:
\(V_{bloco}=12\cdot0,008\)
\(V_{bloco}=0,096\ m^3\)
Por fim, sabemos que cabem 60 blocos no veículo de transporte, então o volume máximo da carga é de:
\(V_{máximo}=0,096⋅60=5,76 m^3\)
Por Raul Rodrigues de Oliveira
Professor de Matemática
