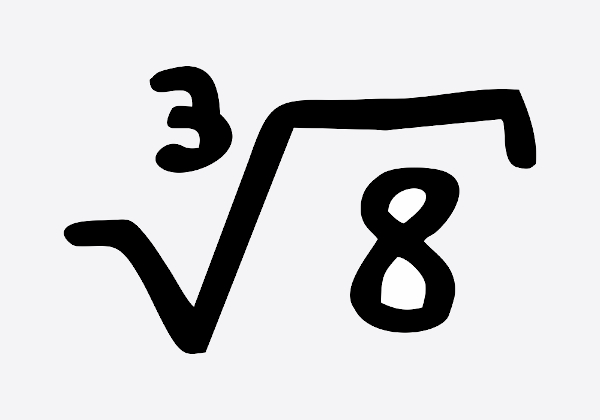PUBLICIDADE
A raiz cúbica é a operação de radiciação que possui índice igual a 3. Calcular a raiz cúbica de um número n é encontrar qual número elevado a 3 resulta em n, isto é, \(\sqrt[3]{a}=b\rightarrow b^3=a\). Sendo assim, a raiz cúbica é um caso particular de radiciação.
Saiba mais: Raiz quadrada — como calcular?
Tópicos deste artigo
- 1 - Representação da raiz cúbica de um número
- 2 - Como calcular a raiz cúbica?
- 3 - Lista com as raízes cúbicas exatas
- 4 - Cálculo da raiz cúbica por aproximação
- 5 - Exercícios resolvidos sobre raiz cúbica
Representação da raiz cúbica de um número
Conhecemos como raiz cúbica a operação de radiciação de um número n quando o índice é igual a 3. De modo geral, a raiz cúbica de n é representada por:
\(\sqrt[3]{n}=b\)
-
3 → índice da raiz cúbica
-
n → radicando
-
b → raiz
Como calcular a raiz cúbica?
Sabemos que a raiz cúbica é uma radiciação com índice igual 3, então calcular a raiz cúbica de um número n é procurar qual número multiplicado por ele mesmo três vezes é igual a n. Ou seja, procuramos um número b tal que b³ = n. Para calcular a raiz cúbica de um número grande, podemos realizar a fatoração do número e agrupar as fatorações como potências de expoente igual a 3 para que seja possível simplificar a raiz cúbica.
-
Exemplo 1:
Calcule \(\sqrt[3]{8}\).
Resolução:
Sabemos que \(\sqrt[3]{8}=2\), pois 2³ = 8.
-
Exemplo 2:
Calcule: \(\sqrt[3]{1728}.\)
Resolução:
Para calcular a raiz cúbica de 1728, primeiramente faremos a fatoração de 1728.
Então, temos que:
\(\sqrt[3]{1728}=\sqrt[3]{2^3\cdot2^3\cdot3^3}\)
\(\sqrt[3]{1728}=2\cdot2\cdot3\)
\(\sqrt[3]{1728}=12\)
-
Exemplo 3:
Calcule o valor de \(\sqrt[3]{42875}\).
Resolução:
Para encontrar o valor da raiz cúbica de 42875, é necessário fatorar esse número:
Então, temos que:
\(\sqrt[3]{42875}=\sqrt[3]{5^3\cdot7^3}\)
\(\sqrt[3]{42875}=5\cdot7\)
\(\sqrt[3]{42875}=35\)
Lista com as raízes cúbicas exatas
-
\( \sqrt[3]{0}=0\)
-
\( \sqrt[3]{1}=1\)
-
\( \sqrt[3]{8}=2\)
-
\( \sqrt[3]{27}=3\)
-
\( \sqrt[3]{64}=4\)
-
\( \sqrt[3]{125}=5\)
-
\( \sqrt[3]{216}=6\)
-
\( \sqrt[3]{343}=7\)
-
\( \sqrt[3]{512}=8\)
-
\( \sqrt[3]{729}=9\)
-
\( \sqrt[3]{1000}=10\)
-
\( \sqrt[3]{1331}=11\)
-
\( \sqrt[3]{1728}=12\)
-
\( \sqrt[3]{2197}=13\)
-
\( \sqrt[3]{2744}=14\)
-
\( \sqrt[3]{3375}=15\)
-
\( \sqrt[3]{4096}=16\)
-
\( \sqrt[3]{4913}=17\)
-
\( \sqrt[3]{5832}=18\)
-
\( \sqrt[3]{6859}=19\)
-
\( \sqrt[3]{8000}=20\)
-
\( \sqrt[3]{9281}=21\)
-
\( \sqrt[3]{10648}=22\)
-
\( \sqrt[3]{12167}=23\)
-
\( \sqrt[3]{13824}=24\)
-
\( \sqrt[3]{15625}=25\)
-
\( \sqrt[3]{125000}=50\)
-
\( \sqrt[3]{1000000}=100\)
-
\( \sqrt[3]{8000000}=200\)
-
\( \sqrt[3]{27000000}=300\)
-
\( \sqrt[3]{64000000}=400\)
-
\( \sqrt[3]{125000000}=500\)
-
\( \sqrt[3]{1000000000}=1000\)
Importante: O número que possui raiz cúbica exata é conhecido como um cubo perfeito. Logo, os cubos perfeitos são 0, 1, 8, 27, 64, 125, 216 etc.
Cálculo da raiz cúbica por aproximação
Quando a raiz cúbica não é exata, podemos utilizar a aproximação para encontrar o valor decimal que representa a raiz. Para isso, é necessário descobrir entre quais cubos perfeitos o número se encontra. Determinamos, então, o intervalo em que a raiz cúbica está, e, por fim, descobriremos a parte decimal por tentativa, analisando a variabilidade da parte decimal.
-
Exemplo:
Calcule \(\sqrt[3]{50}\).
Resolução:
Inicialmente, encontraremos entre quais cubos perfeitos o número 50 se encontra:
27 < 50 < 64
Calculando a raiz cúbica dos três números:
\(\sqrt[3]{27}<\sqrt[3]{50}<\sqrt[3]{64}\)
\(3<\sqrt[3]{50}<4\)
A parte inteira da raiz cúbica de 50 é 3 e está entre 3,1 e 3,9. Logo, analisaremos o cubo de cada um desses números decimais, até passar de 50.
3,1³ = 29,791
3,2³ = 32,768
3,3³ = 35,937
3,4³ = 39,304
3,5³ = 42,875
3,6³ = 46,656
3,7³ = 50,653
Então, temos que:
\(\sqrt[3]{50}\approx3,6\) por falta.
\(\sqrt[3]{50}\approx3,7\) por excesso.
Saiba também: Cálculo de raízes não exatas — como fazer?
Exercícios resolvidos sobre raiz cúbica
(IBFC 2016) O resultado da raiz cúbica do número 4 ao quadrado é um número entre:
A) 1 e 2
B) 3 e 4
C) 2 e 3
D) 1,5 e 2,3
Resolução:
Alternativa C
Sabemos que 4² = 16, então queremos calcular \(\sqrt[3]{16}\). Os cubos perfeitos que conhecemos próximos a 16 são 8 e 27:
\(8<16<27\)
\(\sqrt[3]{8}<\sqrt[3]{16}<\sqrt[3]{27}\)
\(2<\sqrt[3]{16}<3\)
Assim, a raiz cúbica de 4 ao quadrado está entre 2 e 3.
Questão 2
A raiz cúbica de 17576 é igual a:
A) 8
B) 14
C) 16
D) 24
E) 26
Resolução:
Alternativa E
Fatorando 17576, temos que:
Portanto:
\(\sqrt[3]{17576}=\sqrt[3]{2^3\cdot{13}^3}\)
\(\sqrt[3]{17576}=2\cdot13\)
\(\sqrt[3]{17576}=26\)
Por Raul Rodrigues de Oliveira
Professor de Matemática
