O plano de Argand-Gauss é formado por dois eixos: um vertical (conhecido como eixo imaginário) e um na horizontal (conhecido como eixo real). Nele é possível representar geometricamente números complexos que estão na forma algébrica.
Por meio dessa representação geométrica, é possível desenvolver alguns conceitos, como o módulo e o argumento de um número complexo. Os números complexos são representados algebricamente por z = a + bi, então eles são representados por pontos (a, b), representação essa que recebe o nome de afixo.
Leia também: Representação geométrica da soma de números complexos
Tópicos deste artigo
- 1 - Representação geométrica de números complexos
- 2 - Afixo
- 3 - Módulo de um número complexo
- 4 - Argumento de um número complexo
- 5 - Exercícios resolvidos
Representação geométrica de números complexos
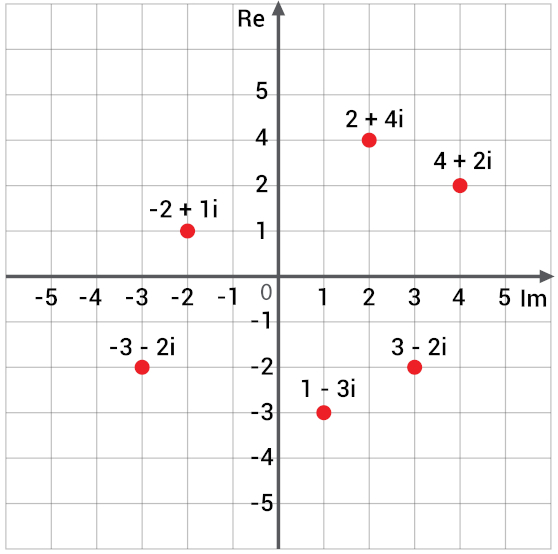
O plano complexo, conhecido também como plano de Argand-Gauss, nada mais é do que um plano cartesiano para números complexos. No plano de Argand-Gauss, é possível representar um número complexo como um ponto, conhecido como afixo. Com o desenvolvimento do plano complexo, há o desenvolvimento da geometria analítica para os números complexos, o que torna possível desenvolver conceitos importantes, como módulo e argumento.
Um número complexo representado em sua forma algébrica é z = a+bi, em que a é a parte real e b é a parte imaginária. Sendo assim, os números complexos são representados como um ponto (a, b). No plano de Argand-Gauss, o eixo horizontal é o eixo da parte real e o eixo vertical é o eixo da parte imaginária.
Afixo
O ponto no plano que representa um número complexo também recebe o nome de afixo. Há três casos possíveis de representação: afixos imaginários, afixos reais e afixos imaginários puros.
-
Afixos imaginários
Um afixo é conhecido como imaginário quando o número complexo possui tanto a parte real quanto a parte imaginária diferentes de zero. Nesse caso o afixo é um ponto em qualquer um dos quatro quadrantes, dependendo dos valores de a, b e seus respectivos sinais.
Exemplo:
Veja a representação dos números complexos z1 = 2 +3i, z2 = -3 - 4i, z3 = -2 + 2i e z4= 1 - 4i.
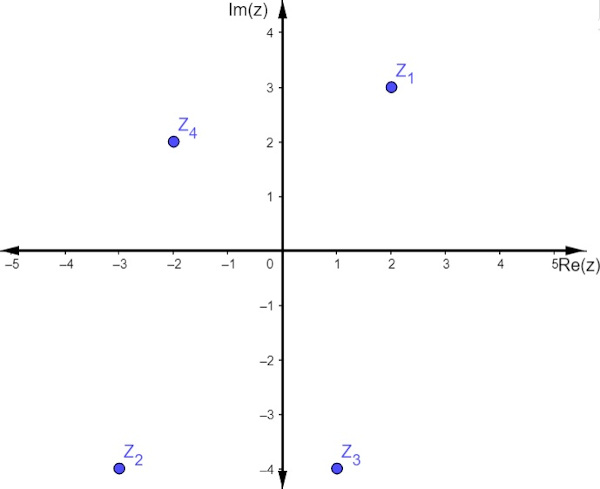
Veja também: Propriedades envolvendo números complexos
-
Afixos imaginários puros
Um número complexo é conhecido como um imaginário puro, quando a sua parte real é igual a zero, ou seja, z = bi. Note que, nesse caso, a primeira coordenada é sempre zero, então vamos trabalhar com pontos do tipo (0, b). Ao marcar no plano de Argand-Gauss, um afixo imaginário puro sempre será um ponto pertencente ao eixo imaginário, ou seja, ao eixo vertical.
Exemplo:
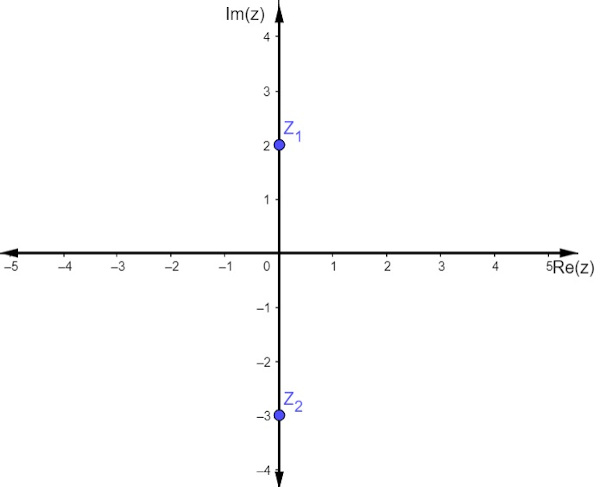
Veja a representação dos números complexos z1 = 2i e z2= -3i.
-
Afixos reais
Um número complexo é classificado como um número real, quando a sua parte imaginária é igual a zero, ou seja, z = a. Nesse caso, a segunda coordenada é sempre zero, então vamos trabalhar com pontos do tipo (a,0), logo a parte imaginaria é zero e os afixos estão contidos no eixo real do plano complexo.
Exemplo:
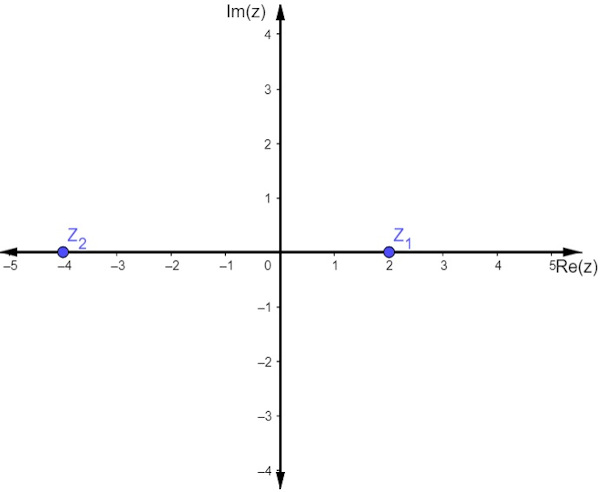
Veja a representação dos números complexos z1 = 2 e z2 = -4.
Módulo de um número complexo
Ao representar um número complexo, seja P (a,b) o afixo do número complexo z = a + bi. Conhecemos como módulo do número complexo a distância do ponto P até a origem. O módulo de um número complexo z é representado por |z|. Para encontrar o valor do |z|, utilizamos o teorema de Pitágoras.
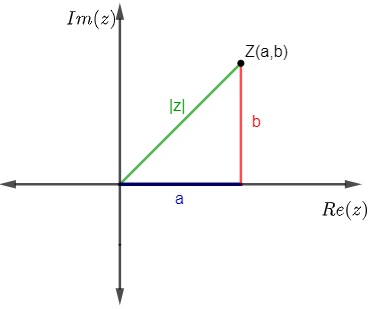
|z|² =a²+b²
Podemos representar também por:
![]()
Exemplo:
Calcule o módulo do número complexo z = 12 -5i.
|z|² = 12² + (-5)²
|z|² 144 + 25
|z|²= 169
|z|=√169
|z| =13
Acesse também: Quais são os números racionais?
Argumento de um número complexo
Conhecemos como argumento de um número complexo o ângulo θ formado pelo vetor OP e o eixo real. O argumento de um número é representado por arg (z) = θ.
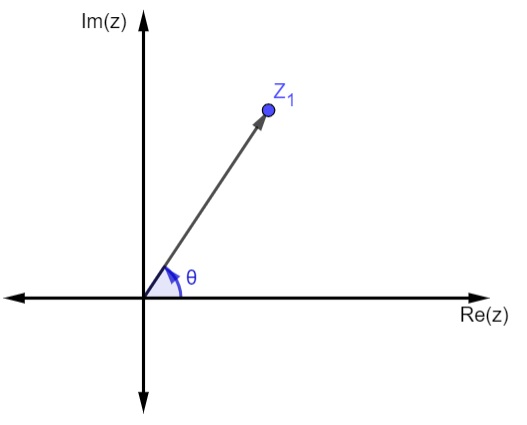
Para encontrar o ângulo, utilizamos as razões trigonométricas seno e cosseno.
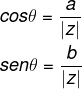
Para encontrar o valor do argumento, conhecendo o seno e o cosseno, basta consultar a tabela dos valores dessas razões trigonométricas. Normalmente, em questões de vestibular sobre esse tema, o argumento é um ângulo notável.
Exemplo:
Calcule o argumento do número complexo z = 1 + i.
Primeiro vamos calcular o módulo de z.
|z|² = 1² + 1²
|z|² = 1+1
|z|² = 2
|z| = √2
Conhecendo |z|, podemos calcular o seno e o cosseno do ângulo.
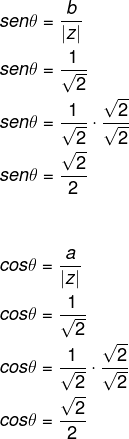
O ângulo que possui seno e cosseno com os valores encontrados é o de 45º.
Exercícios resolvidos
Questão 1 – Qual é o argumento do número complexo z = √3+ i ?
A) 30º
B) 45º
C) 60º
D) 90º
E) 120º
Resolução
Alternativa C.
Sabemos que a = √3 e b = 1, então:
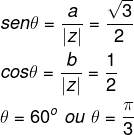
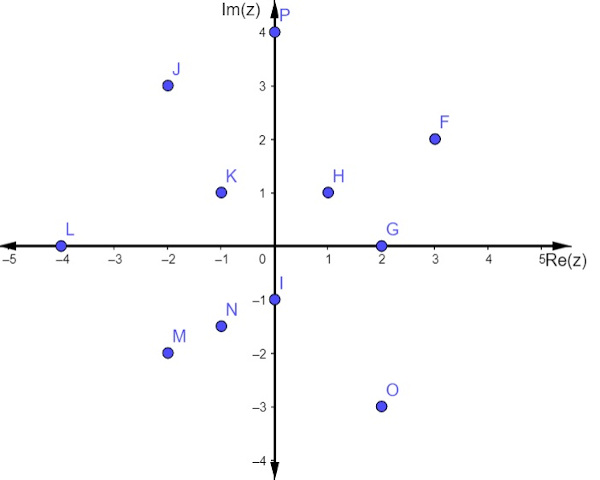
Questão 2 – No plano complexo a seguir, foram representados alguns números. Analisando o plano, podemos afirmar que são representações de números imaginários puros os pontos:
A) M, N e I.
B) P e I.
C) L e G.
D) O, I, G.
E) K, J e L.
Resolução
Alternativa B.
Para identificar um número imaginário puro no plano complexo, é necessário que ele esteja em cima do eixo vertical, que, no caso, são os pontos P e I.
Por Raul Rodrigues de Oliveira
Professor de Matemática

