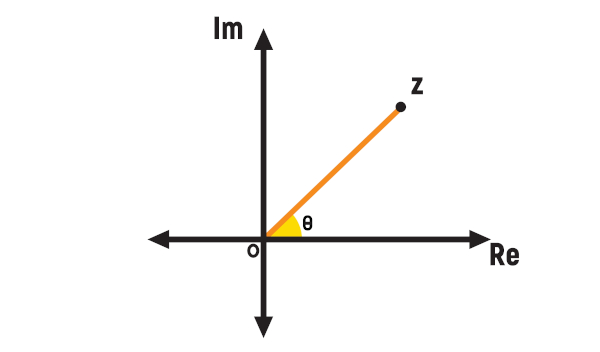
Argumento de um número complexo é o ângulo θ formado com o eixo horizontal e o segmento de reta que liga a representação geométrica de um número complexo à origem do plano de Argand-Gauss. Dado um número complexo da forma x + yi, podemos representá-lo em sua forma geométrica como o ponto Z(x, y).
Quando representamos esse ponto no plano cartesiano, é possível traçar o segmento que vai do ponto Z(x, y) até a origem do plano O(0, 0). Então, para encontrar o valor do ângulo formado pelo segmento de reta OZ e o eixo da parte real do plano no sentido anti-horário, utilizamos as razões trigonométricas seno e cosseno, pois sabendo o valor do seno ou do cosseno do ângulo θ é possível descobrir o valor de θ consultando uma tabela trigonométrica. Em alguns casos, é comum que se trate de um ângulo notável. Representamos o argumento de um número complexo z por arg(z), sendo que arg(z) = θ.
Veja também: Propriedades envolvendo números complexos
Tópicos deste artigo
- 1 - Resumo sobre argumento de um número complexo
- 2 - O que é o argumento de um número complexo?
- 3 - Módulo de um número complexo
- 4 - Como calcular o argumento de um número complexo?
- 5 - Exercícios resolvidos sobre argumento de número complexo
Resumo sobre argumento de um número complexo
-
O argumento de um número complexo z é igual ao ângulo que a representação geométrica desse número faz com o eixo x.
-
Representamos o argumento de z por arg(z) = θ.
-
Para calcular o argumento de z, utilizamos as relações trigonométricas.
O que é o argumento de um número complexo?
Os números complexos podem ser representados no plano complexo, conhecido também como plano de Argand-Gauss. Com a representação geométrica, é possível analisar o número complexo não só de forma algébrica, mas também de forma geométrica.
Dado um número complexo de forma algébrica z = x + yi, ele pode ser representado no plano de pelo ponto Z(x, y). Conhecendo o ponto Z, podemos traçar o segmento OZ, que vai da origem até o ponto em questão. Dessa forma, é possível encontrar o ângulo formado entre o eixo horizontal, conhecido como eixo da parte real, e o segmento de reta OZ. O ângulo formado é igual ao argumento do número complexo. Portanto, dizemos que arg(z) = θ.
Veja, na imagem a seguir, a representação do argumento do número complexo em forma geométrica.
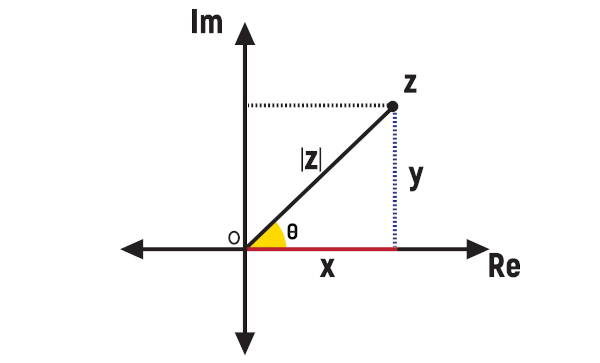
Calcular o argumento de um número complexo é, então, encontrar o ângulo θ. Para isso, é necessário saber calcular o módulo de um número complexo, ou seja, o valor de |z|, pois vamos recorrer à trigonometria para encontrar o valor de arg(z).
-
Videoaula sobre números complexos
Módulo de um número complexo
Para calcular o argumento de um número complexo, é fundamental nos lembrarmos de como se calcula o módulo desse número e o seu significado. Sendo Z(x,y) a representação do número complexo z = x + yi, |z| é igual à distância que esse número se encontra em relação à origem quando representado geometricamente. Assim, |z| será o valor do comprimento do segmento OZ.
Sabemos que |z| é a hipotenusa do triângulo retângulo que possui catetos medindo x e y. Desse modo, para encontrar o valor de |z|, recorremos ao teorema de Pitágoras.
|z|² = x² + y²
Exemplo:
Encontre o |z| do número complexo z = 6 – 8i.
Resolução:
Sabemos que:
x = 6 e y = – 8
Então, calcula-se:
|z|² = x² + y²
|z|² = 6² + ( – 8)²
|z|² = 36 + 64
|z|² = 100
|z| = √100
|z| = 10
Leia também: Representação geométrica da soma de números complexos
Como calcular o argumento de um número complexo?
Utilizamos as razões trigonométricas seno e cosseno do ângulo θ para encontrar o valor do argumento de um número complexo. Elas são iguais ao argumento do número complexo z.
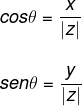
Como os valores de x e y são conhecidos, é necessário calcular o valor de |z| e depois descobrir o valor de cada uma das razões trigonométricas. Conhecendo o valor do seno e do cosseno de θ, é possível encontrar o valor de θ consultando uma tabela trigonométrica.
Exemplo 1:
Qual é o argumento do número complexo z = 1 – i?
Resolução:
Primeiramente, calcularemos |z|:
|z|² = 1² + ( – 1)²
|z|² = 1 + 1
|z|² = 2
|z| = √2
Agora, calcularemos o cosseno de θ:
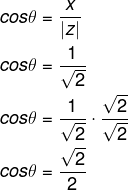
Calcularemos também o valor do seno de θ:
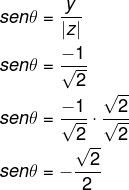
Sabemos que o ângulo que possui seno e cosseno iguais a √2/2 é o ângulo de 45°. Porém, note que o seno é negativo, portanto esse é um ângulo do 4º quadrante. O ângulo simétrico ao ângulo de 45° no 4º quadrante é igual a 360 – 45 = 315°. Assim, temos que:
θ = 315°
Logo, podemos afirmar que arg(z) = 315°.
Exemplo 2:
Calcule o valor do argumento do número complexo √3 + i.
Resolução:
Calculando |z|, temos o seguinte:
|z|² = √3² + 1²
|z|² = 3 + 1
|z|² = 4
|z| = √4
|z| = 2
Agora, calculando o valor do cosseno e do seno desse ângulo, obtém-se:
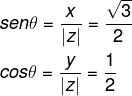
O ângulo que possui seno igual a √3/2 e cosseno igual a 1/2 é o ângulo de 60°. Portanto, temos que arg(z) = 60°.
Leia também: Operações de números complexos na forma trigonométrica
Exercícios resolvidos sobre argumento de número complexo
Questão 1
(Prefeitura do Rio de Janeiro) Um número complexo z tem módulo 2 e argumento 45°. Se z for escrito em sua forma algébrica a + bi, em que a e b são números reais e i é a unidade imaginária, o valor da soma a + b equivale a:
A) 2
B) √3/2
C) √2
D) 2√2
Resolução:
Alternativa D
Sabemos que |z| = 2. Então, temos que:
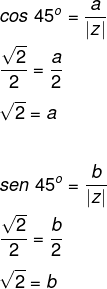
Então, a soma de a + b = √2 + √2 = 2√2.
Questão 2
(Quadrix) Observe o número complexo a seguir, representado graficamente, por meio de um plano de Argand-Gauss.
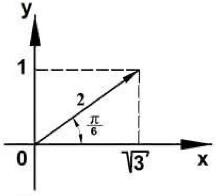
Assinale a alternativa que contém o valor do argumento desse número complexo.
A) √3
B) 1
C) 2
D) 0
E) π/6
Resolução:
Alternativa E
O argumento do número complexo z é igual ao ângulo que ele faz com o eixo horizontal — no caso, igual a π/6.
Por Raul Rodrigues de Oliveira
Professor de Matemática