O conjunto dos números complexos é formado por todos os números z que podem ser escritos na seguinte forma:
z = a + bi
Nessa forma, i = √(– 1). Nesses números, a é chamado de parte real e b é chamado de parte imaginária. Para representar os números complexos geometricamente, utilizaremos vetores no plano.
Representação geométrica de números complexos
Os números complexos podem ser representados geometricamente em um plano construído de forma semelhante ao plano cartesiano: dois eixos perpendiculares que, por sua vez, são retas numéricas. Além disso, essas duas retas encontram-se em suas origens.
A diferença entre esse plano e o plano cartesiano é somente a interpretação: o eixo x desse plano é chamado de eixo real, e o eixo y é chamado de eixo imaginário. Assim, para representar um número complexo nesse plano, conhecido como plano de Argand-Gauss, devemos transformar esse número em um par ordenado, em que a coordenada x é a parte real do número complexo e a coordenada y é sua parte imaginária.
Feito isso, o vetor que representa um número complexo é sempre o segmento de reta orientado que tem início na origem do plano de Argand-Gauss e finda no ponto (a, b), em que a é a parte real do número complexo e b é sua parte imaginária.
Em outras palavras, a maior diferença entre esses planos é que, no plano cartesiano, marcamos pontos e, no plano de Argand-Gauss, usamos a parte real e imaginária dos números complexos para marcar vetores.
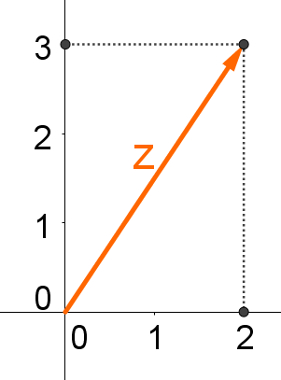
A imagem a seguir mostra a representação geométrica do número complexo z = 2 + 3i.
Representação geométrica da adição de números complexos
Dados os complexos z = a + bi e u = c + di, temos a seguinte adição algébrica:
a + u = a + bi + c + di
a + u = a + c + (b + d)i
Observe que, do pondo de vista geométrico, o que é feito na adição de números complexos é a soma de suas coordenadas em um mesmo eixo.
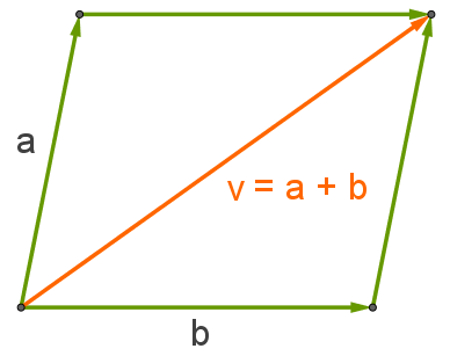
Geometricamente, a soma entre os complexos z = a + bi e u = c + di pode ser feita da seguinte maneira:
1 – Desenhe os vetores z e u no plano de Argand-Gauss;
2 – Transfira uma cópia u’ do vetor u para o ponto final do vetor z. Em outras palavras, desenhe um vetor com o mesmo comprimento do vetor u e paralelo a ele a partir do ponto (a, b).
3 – Transfira uma cópia z’ do vetor z para o ponto final do vetor u;
4 – Observe que os vetores u, u’, z e z’ formam um paralelogramo, e construa um vetor v que parte da origem e finda no encontro entre os vetores u’ e z’.
5 – v = z + u
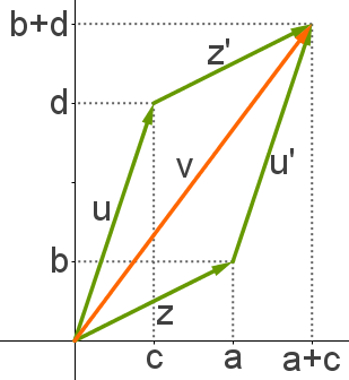
Observe essa construção na imagem a seguir:
O vetor v é justamente a diagonal desse paralelogramo formado pelos vetores u, u’, z e z’.
Exemplo
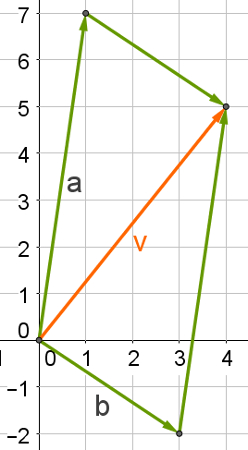
Considere o vetor a = 1 + 7i e o vetor b = 3 – 2i. Veja a construção do paralelogramo a partir desses dois vetores:
Dessa forma, é possível determinar o resultado da soma entre esses dois vetores observando as coordenadas do vetor v = (4, 5). Portanto, o número complexo v = 4 + 5i.
Por Luiz Paulo Moreira
Graduado em Matemática