Frações algébricas

As frações algébricas são expressões algébricas que possuem frações com uma ou mais incógnitas nos seus denominadores, ou seja, há um valor desconhecido, representado por uma letra, no denominador dessas frações.

Para identificar se uma fração é algébrica ou não, basta verificar se há incógnita em seu denominador. Podemos realizar as operações básicas entre frações algébricas, como a adição, a subtração, a multiplicação e a divisão. Quando possível, podemos também realizar a simplificação de uma fração algébrica.

Leia também: Polinômios — expressão algébrica formada por monômios

Tópicos deste artigo

• 1 - Resumo sobre frações algébricas
• 2 - Videoaula sobre frações algébricas
• 3 - O que são frações algébricas?
• 4 - Como identificar uma fração algébrica?
• 5 - Simplificação de frações algébricas
• 6 - Operações com frações algébricas
  • Adição e subtração de frações algébricas
  • Multiplicação de frações algébricas
  • Divisão de frações algébricas
• 7 - Exercícios resolvidos sobre frações algébricas

Resumo sobre frações algébricas

• Frações algébricas são expressões que possuem fração com uma ou mais incógnitas no denominador.
• Podemos realizar a adição, a subtração, a multiplicação e a divisão entre frações algébricas.
• Quando possível, podemos simplificar a fração algébrica.
• Para realizar a multiplicação e a divisão de frações algébricas, utilizamos as propriedades de potência e a simplificação.
• Na adição e na subtração de frações algébricas, é necessário encontrar um múltiplo comum das duas frações.

Videoaula sobre frações algébricas

O que são frações algébricas?

As frações algébricas são expressões algébricas que possuem fração com uma ou mais incógnitas no seu denominador.

Exemplos:

• $\frac{x-1}{x}, com\ x \neq 0$
• $\frac{3x-4}{3+7r}, com\ 3 + 7r \neq 0$
• $\frac{2}{mn+k}, com\ mn\ +\ k\ \neq0$

Como identificar uma fração algébrica?

A identificação de uma fração algébrica dá-se analisando o seu denominador. Se na fração o seu denominador possui incógnita, então ela é algébrica. Podemos ver a presença de frações desse tipo na modelagem de diversas situações, não só da Matemática como também da Física e da Química. São inúmeras as fórmulas que possuem uma incógnita no denominador.

Exemplos:

$D=\frac{m}{V}$ → fórmula da densidade

$P=\frac{F}{A}$ → fórmula de pressão

$F=G\cdot\frac{m_{g1}\cdot m_{g_2}}{d^2}$ → fórmula da força gravitacional

Simplificação de frações algébricas

As técnicas de simplificação de fração são válidas também nas frações algébricas, pois simplificar uma fração algébrica é encontrar uma fração equivalente que seja mais simples. Para realizar a simplificação de frações algébricas, primeiro, fatoramos o numerador e o denominador, e posteriormente simplificamos os fatores que estão tanto no numerador quanto no denominador.

Exemplo 1:

$\frac{12x^5y^3m^2}{10x^3y^4}$

Fatorando o numerador e o denominador, temos que:

$\frac{2\cdot2\cdot3\cdot x\cdot x\cdot x\cdot x\cdot x\cdot y\cdot y\cdot y\cdot m\cdot m}{2\cdot5\cdot x\cdot x\cdot x\cdot y\cdot y\cdot y\cdot y}$

Agora, simplificando os termos semelhantes, temos que:

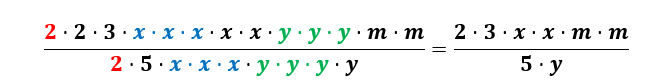
Então a forma simplificada será:

$\frac{6x^2m^2}{5y}$

Exemplo 2:

$\frac{3ab^3}{18b^4}$

Simplificando, temos que:

$\frac{\color{red}{3}\cdot a\color{green}{3\cdot b\cdot b\cdot b}}{\color{red}{3}\cdot 3\cdot{2\cdot \color{green}{b\cdot b\cdot b\cdot b}}}=\frac{a}{2b}$

Para conferir mais exemplos de simplificação de frações algébricas, clique aqui.

Operações com frações algébricas

• Adição e subtração de frações algébricas

Para somar ou subtrair frações algébricas, utilizamos o processo análogo ao das frações sem letras no denominador. Veja os passos a seguir:

• Passo 1: Encontre um denominador comum.

Para somar frações algébricas, é necessário encontrar um denominador comum. Isso envolve fatorar os denominadores e determinar um múltiplo comum entre eles.

• Passo 2: Iguale os denominadores.

Conhecendo o denominador comum, multiplique o numerador e o denominador de cada fração pelo fator necessário para igualar os denominadores.

• Passo 3: Some os numeradores.

Com denominadores iguais, você pode somar ou subtrair os numeradores das duas frações. Basta adicionar os numeradores.

• Passo 4: Simplifique a fração, se possível.

Se possível, simplifique a fração resultante dividindo o numerador e o denominador pelo maior divisor comum.

Exemplo 1:

$\frac{1}{x}+\frac{2}{y}$

O múltiplo comum de x e y é o produto entre eles, ou seja, xy. Então, na primeira fração, multiplicaremos por y o numerador e o denominador, e na segunda fração, por x o numerador e o denominador:

$\frac{1y}{xy}+\frac{2x}{xy}$

Agora somaremos os numeradores:

$\frac{y+2x}{xy}$

Note que, nesse caso, não é possível simplificar a fração algébrica, então a resposta será exatamente essa, ou seja:

$\frac{1}{x}+\frac{2}{y}=\frac{y+2x}{xy}$

Exemplo 2:

$\frac{m}{3}+\frac{n}{m^2}-\frac{mn}{4m}$

Resolução:

O múltiplo em comum será 3⋅4⋅m2. Note que o m é fator comum da primeira e da segunda fração, portanto, pegamos ele com o seu maior expoente, assim, o denominador será 12m².

Logo, temos que:

$\frac{4m^3}{12m^2}+\frac{12n}{12m^2}-\frac{3m^2n}{12m^2}$

$\frac{4m^3+12n-3m^2n}{12m^2}$

Para conferir mais exemplos, clique aqui.

• Multiplicação de frações algébricas

Na multiplicação de frações algébricas, multiplicamos numerador com numerador e denominador com denominador, assim como nas frações. Para multiplicar os termos, utilizamos a multiplicação de monômios.

Exemplo 1:

$\frac{2x}{3y}\cdot\frac{4b}{5xy}$

Multiplicando reto, temos que:

$\frac{2x\cdot4b}{3y\cdot5xy}=\frac{8xb}{15xy^2}$

Exemplo 2:

$\frac{3xy^2}{8mn}\cdot\frac{x^2y^3}{2mn^5}$

Multiplicando reto, temos que:

$\frac{3xy^2\cdot x^2y^3}{8mn\cdot2mn^5}=\frac{3x^3y^5}{16m^2n^6}$

• Divisão de frações algébricas

Na divisão de frações algébricas, assim como nas frações, multiplicamos a primeira fração pelo inverso da segunda fração, logo, se você dominou a multiplicação das frações algébricas, será fácil realizar a divisão delas.

Exemplo 1:

$\frac{1}{x}:\frac{3}{2y}$

Resolução:

Escreveremos o inverso da segunda fração, e calcularemos o produto entre a primeira fração e o inverso da segunda:

$\frac{1}{x}\cdot\frac{2y}{3}=\frac{1\cdot2y}{x\cdot3}=\frac{2y}{3x}$

Exemplo 2:

$\frac{2xy^3}{3mn}:\frac{m^2n}{5xy}=\frac{2xy^3}{3mn}\cdot\frac{5xy}{m^2n}=\frac{10x^2y^4}{6m^3n^2}$

Leia também: Como fatorar uma expressão algébrica

Exercícios resolvidos sobre frações algébricas

Questão 1

Simplificando a expressão a+ba-b-a-ba+b⋅a-bab, encontramos:

A) $4$

B) $\frac{4}{a-b}$

C) $a + b$

D) $\frac{4}{a+b}$

E) $\frac{a^2+b^2}{a+b}$

Resolução:

Alternativa D

Primeiro calcularemos a soma, o múltiplo comum será (a – b) (a + b).

$\left(\frac{\left(a+b\right)\cdot\left(a+b\right)-\left(a-b\right)\cdot\left(a-b\right)}{\left(a-b\right)\left(a+b\right)}\right)\cdot\frac{a-b}{ab}$

$\left(\frac{a^2+2ab+b^2-\left(a^2-2ab\ +b^2\right)}{\left(a-b\right)\left(a+b\right)}\right)\cdot\frac{a-b}{ab}$

$\left(\frac{4ab}{\left(a-b\right)\left(a+b\right)}\right)\cdot\frac{a-b}{ab}$

Note que estamos dividindo e multiplicando por a – b, então temos que:

$\left(\frac{4ab}{\left(a+b\right)}\right)\cdot\frac{1}{ab}$

$\frac{4ab}{a^2b+ab^2}$

Simplificando dividindo por ab o numerador e o denominador, temos que:

$\frac{4}{a+b}$

Questão 2

Marque a alternativa que melhor define uma fração algébrica:

A) Uma fração algébrica é uma fração que possui incógnita no numerador.

B) Uma fração algébrica é uma fração que possui incógnita no denominador.

C) Uma fração algébrica é uma fração que não possui incógnita.

D) Uma fração algébrica é uma fração que possui mesma variável no numerador e denominador.

E) Uma fração algébrica é uma fração cujo resultado é uma incógnita.

Resolução:

Alternativa B

Por definição, a fração é dita algébrica quando ela possui incógnita em seu denominador.

Fontes:

MORGADO, A. C.; WAGNER, E.; JORGE, M. Álgebra I. São Paulo: Livraria Francisco Alves Editora S.A., 1974.