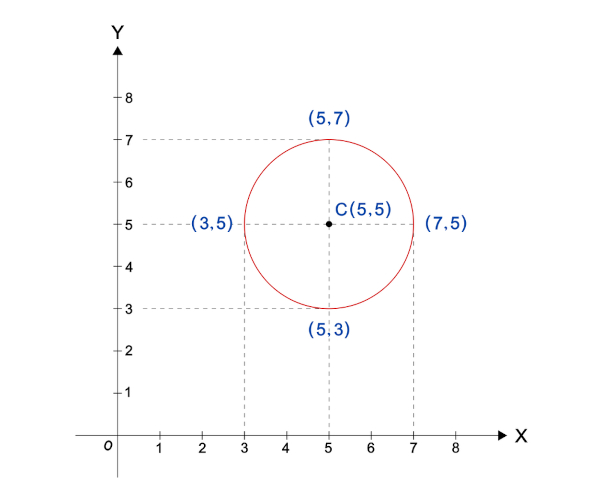
A equação geral da circunferência é objeto de estudo da geometria analítica, que busca descrever de forma algébrica objetos geométricos. Essa equação é obtida quando desenvolvemos as diferenças de quadrados encontradas na equação reduzida, sendo uma equação do tipo x² + y² – 2ax – 2by + a² + b² – r² = 0, em que C(a, b) é o centro da circunferência e r é o raio.
Analisando o gráfico da equação da circunferência, também é possível encontrar a equação geral por meio do valor do seu centro e do seu raio.
Leia também: Equação reduzida da circunferência — aprenda a determiná-la
Tópicos deste artigo
- 1 - Qual é a equação geral da circunferência?
- 2 - Passo a passo para calcular a equação geral da circunferência
- 3 - Como calcular o centro e o raio da circunferência?
- 4 - Exercícios resolvidos
Qual é a equação geral da circunferência?
No estudo da geometria analítica, é bastante comum realizar a análise de objetos geométricos e buscar descrevê-los por meio de uma equação. Com o estudo específico para a circunferência, foram desenvolvidos dois tipos de equações: a equação geral e a equação reduzida. A equação geral é a seguinte:
|
x² + y² – 2ax – 2by + a² + b² – r² = 0 |
Essa equação geral é deduzida a partir da equação reduzida. Vejamos a representação da circunferência de centro C(a,b) e raio r no plano cartesiano:
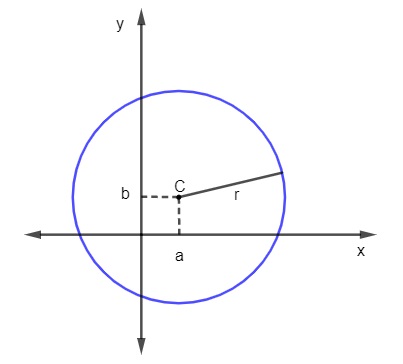
Essa circunferência possui centro C(a,b) e raio r, então a sua equação reduzira é:
(x – a) ² + (y – b)² = r²
Note que existem dois quadrados da diferença na equação e podemos desenvolvê-los para encontrar a equação geral da circunferência:
(x – a)² = x² – 2ax + a²
(y – b)² = y² – 2by + b²
Substituindo na equação, temos que:
x² – 2ax + a² + y² – 2bx + b² = r²
Agora vamos passar o r² para o primeiro membro e reordenar os termos para encontrar a equação geral da circunferência:
x² + y² – 2ax – 2by + a² + b² – r² = 0
Passo a passo para calcular a equação geral da circunferência
Para encontrar a equação geral de uma circunferência representada no plano cartesiano, basta seguir alguns passos.
-
1º passo: identificar o centro e o raio da circunferência.
-
2º passo: substituir na equação geral da circunferência os valores encontrados anteriormente.
Exemplo:
Encontre a equação geral da circunferência a seguir:
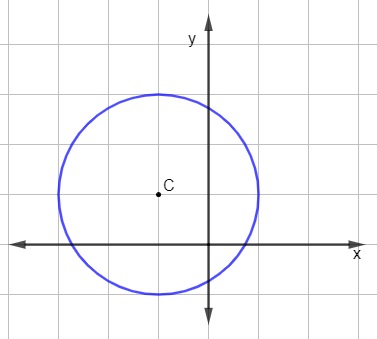
Resolução:
Analisando a representação da circunferência, o ponto C possui coordenadas C( – 1, 1) e, do centro até uma extremidade, há 2 unidades, logo o raio é igual a 2.
Agora que conhecemos o centro e o raio, temos que a = – 1, b = 1 e r = 2. Substituindo na fórmula da equação geral:
x² + y² – 2ax – 2by + a² + b² – r² = 0
x² + y² – 2· ( – 1) · x – 2 · 1 · y + (– 1)² + 1² – 2² = 0
Agora realizaremos a operação até encontrar a equação:
x² + y² + 2x – 2y + 1 + 1 – 4 = 0
x² + y² + 2x – 2y – 2 = 0
Logo, a equação geral dessa circunferência é: x² + y² + 2x – 2y – 2 = 0.
Leia também: Diferenças entre círculo e circunferência
Como calcular o centro e o raio da circunferência?
Dada a equação da circunferência, é possível encontrar o centro e o raio por meio do método da comparação. Vejamos na prática como fazer isso.
Exemplo:
Encontre o centro e o raio da circunferência com equação geral x² + y² + 8x – 2y + 1= 0.
Resolução:
Sabemos que a equação geral da circunferência é x² + y² – 2ax – 2by + a² + b² – r² = 0. Queremos encontrar o valor de (a,b) e, para isso, vamos comparar os termos da equação:
– 2ax = 8x
– 2a = 8
a = 8 : ( – 2)
a = – 4.
Também temos que:
– 2by = – 2y
– 2b = – 2
b = – 2 : ( – 2)
b = 1
Agora que conhecemos o valor de a e b, vamos analisar o termo independente:
a² + b² – r² = 1
( – 4)² + 1² – r² = 1
16+1 – r² = 1
17 – r² = 1
17 – 1 = r²
16 = r²
r = √16
r = 4
Exercícios resolvidos
Questão 1
Conhecendo a circunferência x² + y² – 6x +8y +5 = 0, o raio dessa circunferência é igual a:
A) 2√5
B) 50
C) 20
D) 10
E) √2
Resolução:
Alternativa A.
Queremos encontrar o raio r da equação. Para isso, é necessário antes encontrar o valor de a e b.
Sabemos que:
2ax = – 6x
2a = – 6
a = – 6 : 2
a = – 3
Agora encontraremos o valor de b:
2by = 8y
2b = 8
b = 8 : 2
b = 4
Agora encontraremos o valor de r:
a² + b² – r² = 5
( – 3)² + 4² – r² = 5
9 + 16 – r² = 5
25 – r² = 5
25 – 5 = r²
20 = r²
r² = 20
r = √20
r = 2√5
Questão 2
A equação geral da circunferência que possui raio 7 e centro C( -5,2) é?
A) x² + y² + – 3 = 7
B) (x + 5)² + (y – 2)² = 49
C) (x – 5)² + (y – 2)² = 1
D) x² + y² + 10x – 4y – 20 = 0
E) x² + y² + 10x +4y + 20 = 0
Resolução:
Alternativa D.
Sabemos que a fórmula da equação geral é:
x² + y² – 2ax – 2ay + a² + b² – r² = 0
Sabemos que a = – 5, b = 2 e r = 7.
Substituindo na fórmula, temos que:
x² + y² – 2 · ( – 5) · x – 2 · 2 · y + (– 5)² + 2² – 7² = 0
x² + y² + 10x – 4y + 25 + 4 – 49 = 0
x² + y² + 10x – 4y – 20 = 0
Por Raul Rodrigues de Oliveira
Professor de Matemática