Binômio de Newton é qualquer binômio elevado a um número n em que n é um número natural. Graças aos estudos do físico Isaac Newton sobre as potências de binômios, foi possível verificar regularidades que facilitam a representação do polinômio gerado a partir da potência de um binômio.
Observadas essas regularidades, tornou-se possível também encontrar somente um dos termos do polinômio, sem ter que calculá-lo todo, utilizando a fórmula do termo geral de um binômio. Além disso, Newton percebeu uma relação entre a análise combinatória e os binômios de Newton, o que fez do triângulo de Pascal uma ótima ferramenta para o desenvolvimento mais prático de um binômio de Newton.
Leia também: Dispositivo de Briot-Ruffini – método para divisão de polinômios
Tópicos deste artigo
Definição de binômio de Newton
Definimos como binômio o polinômio que possui dois termos. Em algumas aplicações na Matemática e na Física, é necessário calcular potências de um binômio. Para facilitar o processo, Isaac Newton percebeu regularidades importantes que nos permitem encontrar o polinômio que resulta da potência de um binômio.

Para alguns casos, o cálculo é bastante simples: basta realizar a multiplicação do binômio por ele mesmo utilizando a propriedade distributiva. Até uma potência de ordem 3, desenvolvemos sem muito esforço, pois são os conhecidos produtos notáveis, mas, para potências maiores, calcular a partir da multiplicação do termo por ele mesmo n vezes é bastante trabalhoso.
Exemplos
Vale lembrar que todo número elevado a zero é igual a 1 e que todo número elevado a 1 é ele mesmo, o que vale também para os binômios.
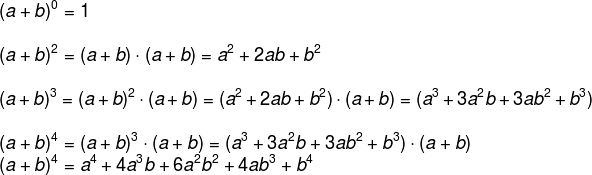
Newton percebeu uma relação entre os coeficientes de cada um dos termos e a combinação, o que permitiu o cálculo de uma potência de um binômio de forma mais direta a partir da seguinte fórmula:
![]()
Entendendo a fórmula:
Primeiro vamos analisar a parte literal de cada termo, que é a letra com o seu expoente. Note que, para cada termo, o expoente de “a” foi diminuindo, começando em n, depois foi para n – 1, e assim sucessivamente até ser 1 no penúltimo termo e 0 no último termo (o que faz com que a letra “a” nem apareça no último termo).
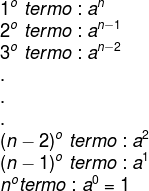
Identificando a e seus expoentes:
Agora vamos analisar os expoentes de “b”, que vão sempre aumentando, começando com 0 no primeiro termo (o que faz a letra b nem aparecer no primeiro termo), 1 no segundo termo, e assim sucessivamente até ser igual a n no último termo.

Identificando b e seus expoentes:
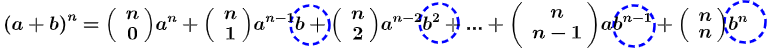
Entendendo a parte literal, vamos analisar os coeficientes, que são todas as combinações de n elementos tomados de 0 em 0, 1 em 1, 2 em 2, e assim sucessivamente até o último termo, que é a combinação de n elementos tomados de n em n.
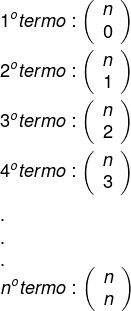
Vale ressaltar que é importante o domínio do cálculo das combinações para conseguir encontrar os coeficientes. Lembre-se de que, para calcular combinações, temos que:
![]()
A resposta da combinação é sempre um número natural.
Veja também: Divisão de polinômios: como resolver?
Exemplo: Calcule o binômio de Newton (a+b) elevado à quarta potência.
1º passo: escrever o polinômio utilizando a fórmula.
![]()
2º passo: calcular as combinações.
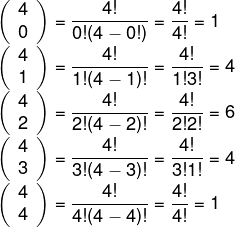
Substituindo as combinações, o polinômio encontrado será:
![]()
É possível perceber que a resolução de casos assim ainda é trabalhosa, dependendo do expoente, mas mesmo assim é mais rápida do que calcular por meio da propriedade distributiva. Uma ferramenta que pode ajudar nesse calculo é o triângulo de Pascal.
Triângulo de Pascal
O triângulo de Pascal foi desenvolvido por Blaise Pascal durante o estudo das combinações. Ele é um caminho que torna os cálculos das combinações mais fácil. A utilização do triângulo de Pascal faz com que seja mais rápido e mais fácil encontrar os coeficientes das partes literais de um binômio de Newton sem ter que calcular todas as combinações.
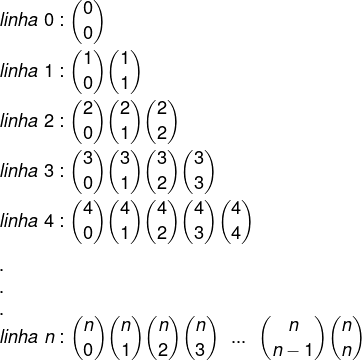
Para construir o triângulo de Pascal de forma direta, vamos lembrar duas situações em que o cálculo da combinação é igual a 1.
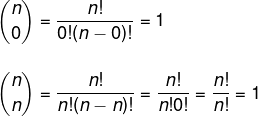
Assim, o primeiro e o último termo de todas as linhas são sempre iguais a 1. Já os termos centrais são construídos a partir da soma do termo que está acima dele mais o seu vizinho da coluna anterior, como na representação abaixo:

Para construir as próximas linhas, basta lembrar que o primeiro termo é 1 e o último também. Depois basta realizar as somas para descobrir os termos centrais.
Acesse também: Teorema da decomposição de um polinômio
Exemplo: Calcule (a+b) elevado à sexta potência.
1º passo: aplicar a fórmula do binômio.
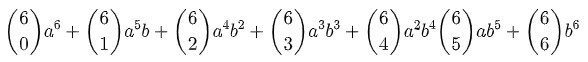
2º passo: construir o triângulo de Pascal até a 6ª linha.
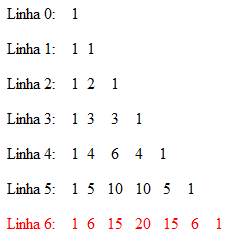
3º passo: substituir as combinações pelos valores da linha 6, que são os coeficientes de cada um dos termos do binômio.
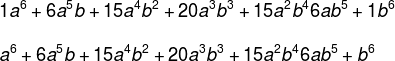
O que determina a quantidade de linhas que vamos construir do binômio é o valor de n. É importante lembrar que a primeira linha é a zero.

Termo geral do binômio de Newton
O termo geral do binômio de Newton é uma fórmula que nos permite calcular um termo do binômio sem precisar desenvolver todo o polinômio, ou seja, podemos identificar qualquer um dos termos do primeiro ao último. Com a fórmula, calculamos diretamente o termo que estamos procurando.
![]()
a: primeiro termo
b: segundo termo
n: expoente
p + 1: termo procurado
Exemplo: Encontre o 11º termo do binômio (a + b)12.
Resolução:
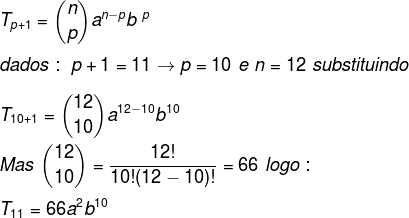
Veja também: Demonstrações por meio do cálculo algébrico
Exercícios resolvidos
Questão 1 – (Cesgranrio) O coeficiente de x4 no polinômio P(x) = (x + 2)6:
a) 64
b) 60
c) 12
d) 4
e) 24
Resolução
Queremos encontrar um termo específico na resolução do binômio; para isso, precisamos encontrar o valor de p.
![]()
Sabemos que o primeiro termo nesse caso é igual a x, então n – p = 4, como n = 6, temos:
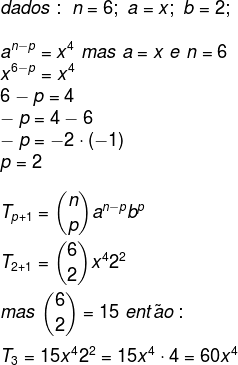
Logo, o coeficiente é 60 (alternativa B).
Questão 2 – (Unifor) Se o termo central do desenvolvimento do binômio (4x + ky)10 for 8064x5y5, então a alternativa que corresponde ao valor de k será:
a)1/4
b)1/2
c) 1
d) 2
e) 4
Resolução: Sabemos que o termo central tem coeficientes iguais (p= 5). Vamos encontrar o 6º termo, pois p+1=6. Além disso, temos que a = 4x; b = ky e n = 10, então:
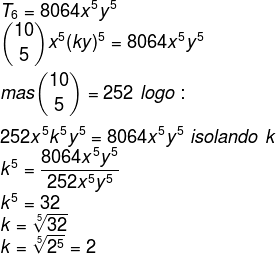
Alternativa D.
Por Raul Rodrigues de Oliveira
Professor de Matemática

