Triângulo de Pascal

O triângulo de Pascal é uma ferramenta bastante antiga da matemática. Ao longo da história, ele recebeu vários nomes, mas os mais adotados atualmente são triângulo aritmético e triângulo de Pascal. O segundo nome é uma homenagem ao matemático que fez várias contribuições no estudo desse triângulo, o que não significa que o triângulo foi inventado por ele, mas foi ele quem fez um estudo mais aprofundado dessa ferramenta.

A partir das propriedades do triângulo de Pascal, é possível realizar a sua construção de forma lógica. Também se destaca a sua relação com combinações estudadas na análise combinatória. Os termos do triângulo de Pascal correspondem também a coeficientes binomiais e, por isso, ele é muito útil para calcularmos qualquer binômio de Newton.

Leia também: Dispositivo de Briot-Ruffini – método para divisão de polinômios

Tópicos deste artigo

• 1 - Construção do triângulo de Pascal
• 2 - Propriedades do triângulo de Pascal
  • 1ª propriedade
  • 2ª propriedade
  • 3ª propriedade
  • 4ª propriedade
  • 5ª propriedade
• 3 - Binômio de Newton
• 4 - Coeficiente binomial
• 5 - Exercícios resolvidos

Construção do triângulo de Pascal

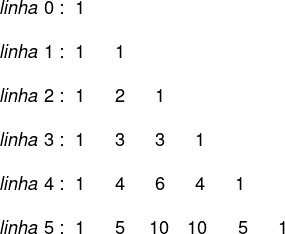
O triângulo de Pascal é produzido a partir do resultado das combinações, porém existe um método prático que facilita a forma de construí-lo. A primeira linha e a primeira coluna são contadas como linha zero e coluna zero. Podemos usar quantas linhas forem necessárias nessa construção, logo o triângulo pode ter infinitas linhas. O raciocínio para a elaboração das linhas é sempre o mesmo. Veja:

Sabemos que os termos do triângulo são combinações, estudadas em análise combinatória. Para substituição do triângulo de Pascal por valores numéricos, sabemos que as combinações de um número com zero e de um número com ele mesmo são sempre iguais a 1. Sendo assim, o primeiro e o último valor são sempre 1.

Para encontrar os demais, começamos pela linha 2, já que a linha 0 e a linha 1 já estão completas. Na linha 2, para encontrar a combinação de 2 para 1, na linha acima, ou seja, na linha 1, vamos somar o termo acima dele na mesma coluna e o termo acima dele na coluna anterior, conforme na imagem:

Após construir a linha 2, é possível construir a linha 3 realizando o mesmo procedimento.

Continuando esse procedimento, encontraremos todos os termos – neste caso, até a linha 5 –, mas é possível construir quantas linhas forem necessárias.

Propriedades do triângulo de Pascal

Existem algumas propriedades do triângulo de Pascal, em razão da regularidade em sua construção. Essas propriedades são úteis para trabalhos com combinações, a própria construção das linhas do triângulo e a soma de linhas, colunas e diagonais.

• 1ª propriedade

A primeira propriedade foi a que usamos para construir o triângulo. Assim, para encontrar um termo no triângulo de Pascal, basta realizar a soma do termo que está na linha acima dele e mesma coluna com o termo que está na coluna e linha anteriores a ele. Essa propriedade pode ser representada da seguinte maneira:

Essa propriedade é conhecida como relação de Stifel e é importante por facilitar a construção do triângulo e encontrarmos os valores de cada uma das linhas.

• 2ª propriedade

A soma de todos os termos de uma linha é calculada por:

S_n=2ⁿ, em que n é o número da linha.

Exemplos:

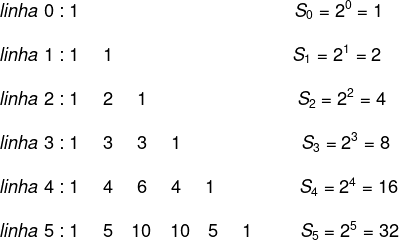
Com essa propriedade, é possível saber a soma de todos os termos de uma linha sem precisar necessariamente construir o triângulo de Pascal. A soma da linha 10, por exemplo, pode ser calculada por 2¹⁰ = 1024. Ainda que não se conheçam todos os termos, já é possível saber o valor da soma de toda a linha.

• 3ª propriedade

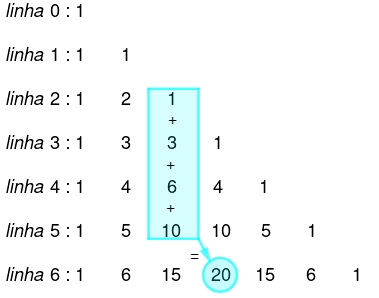
A soma dos termos que sequencia desde o começo uma determinada coluna p até uma determinada linha n é igual ao termo que está na linha n+1 posterior e coluna p+1 posterior, como é mostrado a seguir:

• 4ª propriedade

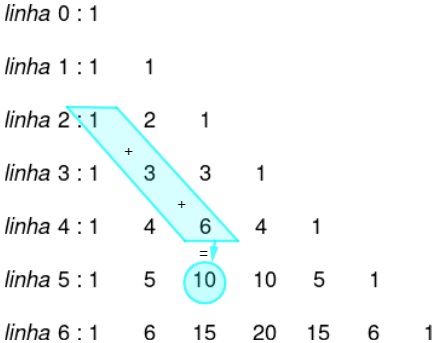
A soma de uma diagonal que começa na coluna 0 e vai até o termo que se encontra na coluna p e linha n é igual ao termo que está na mesma coluna (p), mas na linha abaixo (n+1), como mostrado na imagem:

• 5ª propriedade

Existe uma simetria nas linhas do triângulo de Pascal. O primeiro e o segundo termo são iguais, o segundo e o penúltimo são iguais e assim sucessivamente.

Exemplo:

Linha 6: 1 6 15 20 15 6 1.

Note que os termos são iguais dois a dois, exceto o termo central.

Veja também: Divisão de polinômios: como resolver?

Binômio de Newton

Definimos como binômio de Newton a potência de um polinômio que possui dois termos. O calculo de um binômio está relacionado com o triângulo de Pascal, que se torna um mecanismo para calcular o que chamamos de coeficientes binomiais. Para calcular um binômio, usamos a seguinte fórmula:

Note que o valor do expoente de a vai diminuindo até que no último termo ele seja igual a a⁰. Sabemos que todo número elevado a 0 é igual a 1, por isso o termo a não aparece no último termo. Perceba também que o expoente de b começa com b⁰, logo b não aparece no primeiro termo e vai aumentando até chegar a bⁿ, no último termo.

Além disso, o número que acompanha cada um dos termos é o que chamamos de coeficiente – neste caso, conhecido como coeficiente binomial. Para compreender melhor como resolver esse tipo de binômio, acesse o nosso texto: Binômio de Newton.

Coeficiente binomial

O coeficiente binomial nada mais é do que a combinação, que pode ser calculada pela fórmula:

Porém, para facilitar o calculo do binômio de Newton, é essencial o uso do triângulo de Pascal, já que ele nos dá o resultado da combinação de forma mais rápida.

Exemplo:

Para encontrar o resultado do coeficiente binomial, vamos encontrar os valores da linha 5 do triângulo de Pascal, que são {1,5,10,10,5,1}.

(x+y)⁵= 1x⁵+5x⁴y+10x³y²+ 10x²y³ + 5xy⁴+1y⁵

Simplificando:
(x+y)⁵= x⁵+5x⁴y+10x³y²+ 10x²y³ + 5xy⁴+y⁵

Exercícios resolvidos

Questão 1 - O valor da expressão abaixo é?

A) 8

B) 16

C) 2

D) 32

E) 24

Resolução

Alternativa A.

Reagrupando os valores positivos e os valores negativos, temos que:

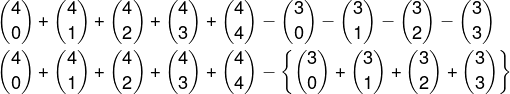
Note que estamos, na verdade, calculando a subtração entre a linha 4 e a linha 3 do triângulo de Pascal. Pela propriedade, sabemos que:

S₄ = 2⁴ = 16

S₃= 2³ = 8

16 – 8 = 8.

Questão 2 - Qual é o valor da expressão abaixo?

A) 32

B) 28

C) 256

D) 24

E) 54

Resolução

Alternativa B.

Note que estamos somando os termos da coluna 1 do triângulo de Pascal até a linha 7, logo, pela 3ª propriedade, o valor dessa soma é igual ao termo que ocupa a linha 7+1 e a coluna 1+1, ou seja, linha 8, coluna 2. Como queremos só um valor, construir o triângulo de Pascal todo não é conveniente.

Por Raul Rodrigues de Oliveira
Professor de Matemática