Combinação simples

A combinação simples é um entre os agrupamentos estudados na análise combinatória. Conhecemos como combinação a contagem de todos os subconjuntos de k elementos que podemos formar de um conjunto de n elementos.

É bastante comum ver situações em que utilizamos a combinação, por exemplo, para calcular todos os resultados possíveis em jogos de loteria ou em jogos de poker, e em outras situações, como no estudo da probabilidade e da estatística.

Outro agrupamento bastante comum é o arranjo. O que diferencia o arranjo da combinação é o fato de que, no arranjo, a ordem dos elementos é importante, e na combinação, a ordem não é importante. Por isso, comparamos a combinação com a escolha de subconjuntos.

Leia também: Princípio fundamental da contagem – utilizado para quantificar as possibilidades

Tópicos deste artigo

• 1 - O que é a combinação simples?
• 2 - Fórmula da combinação simples
• 3 - Como calcular uma combinação?
• 4 - Exemplo:
• 5 - Triângulo de Pascal
• 6 - Diferença entre arranjo e combinação
• 7 - Exercícios resolvidos

O que é a combinação simples?

Na análise combinatória, estuda-se a quantidade de agrupamentos possíveis. Entre esses agrupamentos, existe o conhecido como combinação simples. A combinação simples nada mais é que a contagem de todos os subconjuntos com k elementos de um determinado conjunto, por exemplo: a megassena, em que há um sorteio de 6 números de forma aleatória.

Nesse caso, é possível perceber que a ordem em que esses 6 números foram escolhidos não faz diferença, ou seja, a ordem não importa, o que torna esse resultado um subconjunto. Essa característica é fundamental para compreender-se o que é uma combinação e diferenciá-la dos demais agrupamentos — na combinação, a ordem dos elementos do conjunto não importa.

Fórmula da combinação simples

Os problemas envolvendo combinação são calculados por uma fórmula. A combinação de n elementos tomados de k em k é:

n → total de elementos no conjunto

k → total de elementos no subconjunto

Veja também: Princípio aditivo da contagem – união dos elementos de dois ou mais conjuntos

Como calcular uma combinação?

Em primeiro lugar, é importante saber identificar quando um problema é uma combinação. Para exemplificar, encontre todas as combinações possíveis do conjunto {A, B, C, D} com dois elementos:

Listando as combinações com dois elementos, são elas: {A,B}, {A,C}, {A,D}, {B,C}, {B,D} e {C,D}. Nesse caso é possível ver que há 6 combinações possíveis, e vale ressaltar também que os subconjuntos {A,B} e {B,A} são iguais, pois, na combinação, a ordem não é importante.

Acontece que nem sempre é possível listar todas as combinações possíveis ou até mesmo não é necessário, pois o interesse maior está na quantidade de combinações e não na listagem de cada uma delas. Para isso, é bastante prático o uso da fórmula.

Exemplo:

Uma escola fará um sorteio de três ingressos, um para cada aluno, entre os 10 primeiros colocados na olimpíada de matemática. Após a realização da prova e conhecendo os 10 primeiros colocados, calcule as combinações possíveis para o resultado do sorteio.

Note que, no resultado do sorteio, a ordem não é importante, logo, estamos trabalhando com um problema de combinação.

Calcularemos, então, a combinação de 10 elementos tomados de 3 em 3. Substituindo na fórmula, temos que:

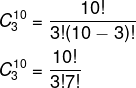
Agora vamos realizar a simplificação dos fatoriais. Nesse momento, é essencial que se domine o cálculo do fatorial de um número. Como 10! é maior que qualquer um dos fatoriais no denominador, e, analisando o denominador, 7! é o maior deles, vamos realizar a multiplicação de 10 pelos seus antecessores até chegar em 7!, para que seja possível simplificar.

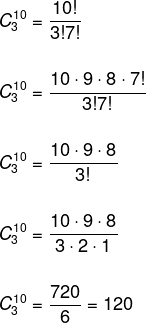
Triângulo de Pascal

Um dos instrumentos bastante utilizados na análise combinatória, principalmente para calcular um binômio de Newton, é o triângulo de Pascal. Esse triângulo é construído dos resultados das combinações, uma outra forma de representar a combinação de dois números é a seguinte:

O triângulo de Pascal começa na linha 0 e coluna 0, pela combinação de 0 elementos tomados de 0 em 0. As linhas são iguais a n, e as colunas iguais a k, formando a seguinte figura:

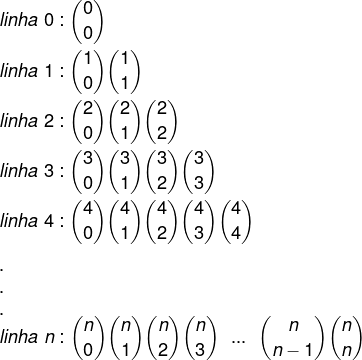
Substituindo pelos valores que são resultados das combinações:

Por meio das linhas e colunas do triângulo de Pascal, é possível encontrar o valor da combinação que desejarmos. Caso necessário, podemos encontrar os termos de quantas linhas forem necessárias. Para saber mais sobre esse método de resolução, leia o texto: Triângulo de Pascal.

Diferença entre arranjo e combinação

O arranjo e a combinação são dois agrupamentos igualmente importantes estudados na análise combinatória. É fundamental saber a diferença entre cada um desses agrupamentos, ou seja, se vamos calculá-los por um arranjo ou uma combinação.

Acontece que, na combinação, ao montar os agrupamentos, a ordem dos elementos do conjunto não é importante, ou seja {A,B} = {B,A}, porém existem casos em que a ordem é importante no agrupamento, nesse caso estamos trabalhando com um arranjo.

No arranjo, então, a ordem dos elementos é diferente, ou seja, {A,B} ≠ {B,A}, um exemplo de arranjo bastante comum seria calcular de quantas maneiras distintas podemos formar o pódio de uma determinada competição entre 10 pessoas. Note que, nesse exemplo, a ordem é importante, o que o torna resolvível pela fórmula de arranjo. Além da definição teórica, as fórmulas são diferentes, e a fórmula do arranjo é:

Exercícios resolvidos

Questão 1 – (Enem) Doze times se inscreveram em um torneio de futebol amador. O jogo de abertura do torneio foi escolhido da seguinte forma: primeiro foram sorteados 4 times para compor o Grupo A. Em seguida, entre os times do Grupo A, foram sorteados 2 times para realizar o jogo de abertura do torneio, sendo que o primeiro deles jogaria em seu próprio campo, e o segundo seria o time visitante. A quantidade total de escolhas possíveis para o Grupo A e a quantidade total de escolhas dos times do jogo de abertura podem ser calculadas através de

A) uma combinação e um arranjo, respectivamente.

B) um arranjo e uma combinação, respectivamente.

C) um arranjo e uma permutação, respectivamente.

D) duas combinações.

E) dois arranjos.

Resolução

Alternativa A

Para diferenciar arranjo e combinação, é necessário analisar se a ordem importa no agrupamento ou não. Note que, no primeiro agrupamento, a ordem é irrelevante, pois o Grupo A é formado pelos 4 times sorteados independentemente da ordem, ou seja, há, primeiro, uma combinação.

Analisando o segundo agrupamento, é possível perceber que nele a ordem importa, pois o primeiro time a ser sorteado terá o mando de campo, o que torna esse agrupamento um arranjo.

Dessa forma, a ordem é uma combinação e um arranjo.

Questão 2 – Uma família composta por 7 pessoas adultas, após decidir o itinerário de sua viagem, consultou o site de uma empresa aérea e constatou que o voo para a data escolhida estava quase lotado. Na figura, disponibilizada pelo site, as poltronas ocupadas estão marcadas com X e as únicas poltronas disponíveis estão em branco.

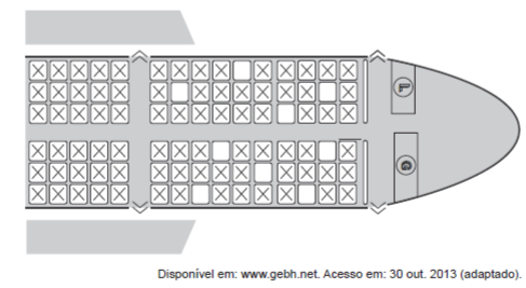
O número de formas distintas de se acomodar a família nesse voo é calculado por:

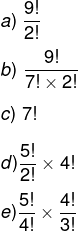
Resolução

Alternativa B. Analisando a situação, note que a ordem, ou seja, qual membro da família sentará em qual cadeira, não é relevante. O que interessa são as 7 poltronas escolhidas pela família. Sendo assim, estamos trabalhando com uma combinação. Há 9 poltronas livres, e 7 serão escolhidas. então, vamos calcular a combinação de 9 para 7. Substituindo na fórmula, temos que:

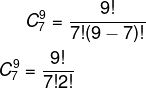
Por Raul Rodrigues de Oliveira
Professor de Matemática