PUBLICIDADE
Observando o Triângulo de Pascal é possível perceber algumas características próprias que são consideradas suas propriedades. Dentre elas destacam-se:
- Primeiro e último elemento de uma linha.
Todas as linhas do triângulo de Pascal terão seu primeiro e seu último elemento igual a 1.
Afirmamos isso, pois o 1º elemento de uma linha é representado por 
= 1 e o último é representado por 
= 1. Sendo que n deve ser sempre um número natural.
- Elementos proporcionais
Essa propriedade afirma que elementos (coeficientes binomiais) eqüidistantes pertencentes a uma mesma linha, possuem valores numéricos iguais. Veja exemplos.
Considere a 3ª linha: .jpg)
Considere a 5ª linha: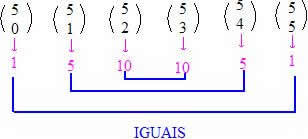 
- Relação de Stifel.
Considerando o triângulo de Pascal representado pelos valores numéricos dos seus elementos (coeficientes binomiais), iremos perceber que a soma de dois elementos de cada linha será igual ao elemento de baixo.
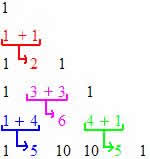
Essa propriedade pode ser representada em forma de equação:
, levando em consideração que n é maior ou igual a p.
- Soma dos elementos de uma linha.
A soma dos elementos de uma linha de numerador n será igual à 2n.
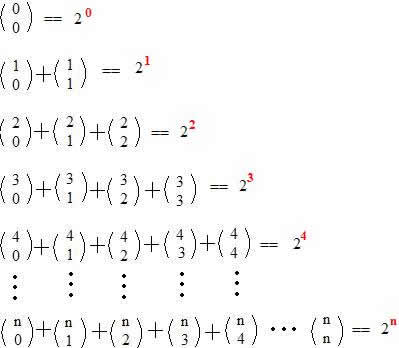
Por Danielle de Miranda
Graduada em Matemática