A análise combinatória é a área da Matemática que estuda e desenvolve técnicas de contagens para resolver diversas situações do nosso cotidiano. Para resolver situações que envolvem análise combinatória, é bastante comum utilizar o princípio fundamental da contagem (PFC). Existem casos de agrupamentos estudados na análise combinatória que recebem nomes especiais e têm fórmulas que nos auxiliam na resolução dessas situações, são eles: a permutação, a combinação e o arranjo.
A análise combinatória exige o entendimento de uma operação essencial chamada fatorial, representada pelo símbolo de exclamação “!”. Determinar o fatorial de um número consiste em calcular o produto desse número por todos os inteiros positivos que o precedem. Além disso, o uso de fatoriais é indispensável nos cálculos de agrupamentos, que têm grande relevância na área de probabilidade, tornando a análise combinatória uma base necessária para quem deseja se aprofundar os estudos sobre probabilidade. No Enem é bastante recorrente questões que podem ser resolvidas utilizando conhecimentos da análise combinatória.
Leia também: Como calcular uma combinação simples
Tópicos deste artigo
- 1 - Resumo sobre análise combinatória
- 2 - O que é análise combinatória?
- 3 - O que se estuda em análise combinatória?
- 4 - Princípio fundamental da contagem
- 5 - Análise combinatória fatorial
- 6 - Tipos de análise combinatória
- 7 - Fórmulas da análise combinatória
- 8 - Probabilidade x análise combinatória
- 9 - Análise combinatória no Enem
- 10 - Exercícios resolvidos sobre análise combinatória
Resumo sobre análise combinatória
- A análise combinatória é a área da Matemática que estuda as técnicas de contagem aplicadas a diversas situações do cotidiano.
- A análise combinatória é também base para o aprofundamento dos estudos sobre probabilidade.
- Princípio fundamental da contagem (PFC): ferramenta básica para resolver problemas que envolvem múltiplas escolhas ou etapas.
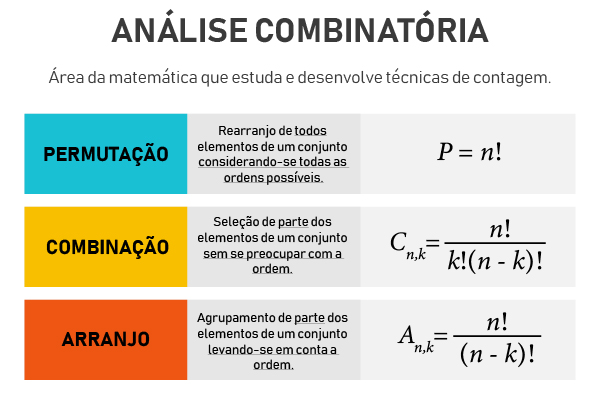
- Existem três agrupamentos importantes estudados na análise combinatória:
- Permutação: Rearranjo dos elementos de um conjunto considerando-se todas as ordens possíveis.
- Combinação: Seleção de parte dos elementos de um conjunto sem se preocupar com a ordem.
- Arranjo: Agrupamento de parte dos elementos de um conjunto levando-se em conta a ordem.
- No Enem é bastante comum ter questões que podem ser resolvidas com análise combinatória.
O que é análise combinatória?
A análise combinatória é uma área da Matemática que estuda o desenvolvimento de técnicas de contagem para resolver problemas do cotidiano, por exemplo, o número de jogadas possíveis em jogos de tabuleiro, o número de combinações possíveis em um cardápio, os resultados possíveis para uma loteria, entre outras várias situações.
O que se estuda em análise combinatória?
Na análise combinatória estudamos tópicos importantes da Matemática, como o princípio fundamental da contagem, os agrupamentos conhecidos como permutação, arranjo e combinação. Estudamos também uma operação importante utilizada para resolver problemas envolvendo análise combinatória conhecida como fatorial.
Veja também: O que é um arranjo com repetição?
Princípio fundamental da contagem
O princípio fundamental da contagem (PFC) é a base da análise combinatória e oferece um método simples e eficaz para calcular o número de possibilidades em situações que envolvem decisões sucessivas. Esse princípio pode ser descrito da seguinte forma:
|
Se uma decisão d1 pode ser tomada de m maneiras e uma decisão d2 pode ser tomada de n maneiras, então o número de maneiras que essas decisões podem ser tomadas simultaneamente é calculado por: N = m · n |
- Exemplo 1:
Uma lanchonete oferece 3 opções de sanduíches (frango, carne ou vegetariano), 2 tipos de bebidas (suco ou refrigerante), 2 sobremesas (sorvete ou pudim). Quantas combinações completas (sanduíche, bebida e sobremesa) um cliente pode escolher?
Resolução:
De acordo com o PFC, basta multiplicar o número de escolhas em cada etapa:
3(sanduiches) ⋅ 2(bebidas) ⋅ 2(sobremesas)
3 ⋅ 2 ⋅ 2 = 12 combinações possíveis.
- Exemplo 2:
Uma pessoa tem 2 camisetas (azul e vermelha) e 3 calças (preta, jeans e branca). Quantos conjuntos diferentes de roupa ela pode montar?
Resolução:
Pelo PFC, basta multiplicar as opções:
2 ⋅ 3 = 6
Análise combinatória fatorial
No estudo da análise combinatória, o fatorial de um número é uma operação matemática importante. Conhecemos como fatorial de um número o produto do número pelos seus antecessores positivos e não nulos, ou seja, maiores que zero. O símbolo do fatorial é o ponto de exclamação “!”, então escrevemos o número seguido do símbolo 4! (lê-se: quatro fatorial). De modo geral, temos que:
\(n! = n \cdot (n-1) \cdot (n-2) \cdot (n-3) \cdots 3 \cdot 2 \cdot 1 \)
Exemplo:
\(4! = 4 \cdot 3 \cdot 2 \cdot 1 = 24 \)
\(6! = 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 720 \)
Tipos de análise combinatória
Existem três agrupamentos importantes estudados na análise combinatória, são eles a permutação, o arranjo e a combinação. Estudaremos cada um deles a seguir:
→ Permutação
Chamamos de permutação os agrupamentos ordenados de todos os elementos de um conjunto. Permutar é trocar de posição, formando uma nova ordem.
A permutação de n elementos é calculada por:
P = n!
- Exemplo 1:
De quantas maneiras diferentes 3 corredores podem ocupar o pódio?
Resolução:
Queremos sabemos quantas ordens possíveis existem para um conjunto com 3 elementos, logo, temos que:
\(P = 3!\)
\(P = 3 \cdot 2 \cdot 1 \)
\(P=6\)
Então há 6 permutações possíveis.
- Exemplo 2:
Quantos anagramas existem com o nome RAUL?
Resolução:
Anagrama é o reordenamento das letras do nome; por exemplo, ARLU, LUAR, RUAL são exemplos de anagramas possíveis. Mas queremos saber mesmo quantos anagramas existem, para isso, basta calcular a permutação de 4 elementos, ou seja:
\(P = 4! = 4 \cdot 3 \cdot 2 \cdot 1 = 24 \)
Há 24 anagramas possíveis.
→ Arranjo
Arranjos são agrupamentos ordenados formados por uma parte dos elementos de um conjunto. Dado um conjunto com n elementos, queremos saber quantos agrupamentos ordenados é possível fazer com k elementos. Para calcular o arranjo, utilizamos a fórmula:
\(A_{n,k} = \frac{n!}{(n-k)!} \)
- Exemplo:
Em uma escola, há 5 alunos (Ana, João, Maria, Pedro e Lucas), e queremos formar um grupo de 3 alunos para representar a escola em uma competição. A ordem dos alunos no grupo importa, ou seja, quem fica em primeiro, segundo e terceiro lugar na competição faz diferença. Quantos diferentes arranjos de 3 alunos podemos formar?
Resolução:
No grupo há 5 pessoas, ou seja, n = 5 e os grupos possuem 3 pessoas, ou seja, k = 3.
\(A_{5,3} = \frac{5!}{(5-3)!} \\ A_{5,3} = \frac{5!}{2!} \\ A_{5,3} = \frac{5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}{2 \cdot 1} \\ A_{5,3} = \frac{120}{2} \\ A_{5,3} = 60 \)
Então há 60 grupos possíveis.
→ Combinação
Conhecemos como combinação todos os subconjuntos que podemos formar com parte dos elementos de um conjunto. Na combinação a ordem dos elementos não é importante, logo, não gera um novo agrupamento. Entendemos como combinação de n, tomados de k em k, a contagem de todos os subconjuntos possíveis com k elementos dentre os n elementos do conjunto. Para calcular as combinações possíveis, utilizamos a fórmula:
\(C_{n,k} = \frac{n!}{k!(n-k)!} \)
- Exemplo:
Em uma loja, há 6 cores diferentes de camisetas (azul, vermelha, verde, amarela, preta e branca) e você quer escolher 2 cores para comprar, mas não importa a ordem das cores. Quantas combinações diferentes de 2 cores você pode escolher?
Resolução:
Sabemos que:
n = 6
k = 2
Então temos que:
\(C_{6,2} = \frac{6!}{2!(6-2)!} \\ C_{6,2} = \frac{6!}{2!4!} \\ C_{6,2} = \frac{6 \cdot 5 \cdot 4!}{2 \cdot 1 \cdot 4!} \)
Simplificando 4! tanto no numerador quanto no denominador:
\(C_{6,2} = \frac{6 \cdot 5}{2} \\ C_{6,2} = \frac{30}{2} \\ C_{6,2} = 15 \)
Então há 15 combinações diferentes de 2 cores de camiseta.
Fórmulas da análise combinatória
Em resumo, temos as seguintes fórmulas:
- Fórmula da permutação: P = n!
- Fórmula do arranjo: \(A_{n,k} = \frac{n!}{(n-k)!}\)
- Fórmula da combinação: \(C_{n,k} = \frac{n!}{k!(n-k)!}\)
Probabilidade x análise combinatória
Probabilidade é uma área superimportante da Matemática que nos ajuda a entender a chance de um evento acontecer. A gente vê probabilidade em várias situações, como nas loterias, nos jogos de dados, nas cartas, entre outros. Para estudar probabilidade de forma completa, é essencial entender bem a análise combinatória, porque a probabilidade de algo acontecer é calculada dividindo a quantidade de casos favoráveis pela quantidade de todos os casos possíveis.
Então, problemas de probabilidade quase sempre envolvem análise combinatória. Isso faz com que a análise combinatória seja fundamental para entender probabilidade, pois ela nos dá as ferramentas para contar os casos favoráveis e os casos possíveis.
Saiba mais: Como fazer uma permutação quando há elementos que se repetem?
Análise combinatória no Enem
Questões envolvendo análise combinatória são recorrentes no Enem. Há questões que cobram desde o princípio fundamental da contagem até questões que envolvem os diferentes os tipos de agrupamentos, como combinação, arranjo e permutação. O que torna essas questões mais desafiadoras é que elas exigem mais atenção na interpretação do problema do que em contas difíceis.
O Enem sempre traz, pelo menos, uma questão desse tema, e muitas vezes o que você precisa é identificar como usar a fórmula, sem necessariamente calcular o valor da combinação ou do arranjo em si. O que o Enem busca é compreender se você consegue identificar qual é o tipo de agrupamento que essa situação descreve.
→ Videoaula sobre análise combinatória no Enem
Exercícios resolvidos sobre análise combinatória
Questão 1
(Enem 2020 – Digital) Eduardo deseja criar um e-mail utilizando um anagrama exclusivamente com as sete letras que compõem o seu nome, antes do símbolo @. O e-mail terá a forma *******@site.com.br e será de tal modo que as três letras “edu” apareçam sempre juntas e exatamente nessa ordem. Ele sabe que o e-mail eduardo@site.com.br já foi criado por outro usuário e que qualquer outro agrupamento das letras do seu nome forma um e-mail que ainda não foi cadastrado.
De quantas maneiras Eduardo pode criar um e-mail desejado?
- 59
- 60
- 118
- 119
- 120
Resolução:
Alternativa D
Sabemos que “edu” aparecerá de novo nessa ordem, logo, vamos permutar 5 elementos (edu, a, r, d, o)
Sabemos que:
\(P_5=5!=5⋅4⋅3⋅2⋅1=120\)
Entretanto, a opção eduardo@site.com.br já foi criada, sendo assim: 120 – 1 = 119.
Questão 2
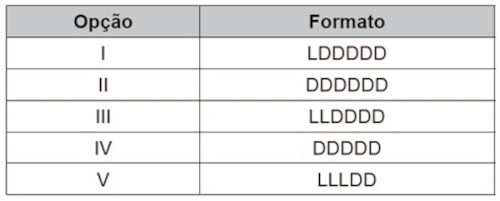
(Enem) Uma empresa construirá sua página na internet e espera atrair um público de aproximadamente um milhão de clientes. Para acessar essa página, será necessária uma senha com formato a ser definido pela empresa. Existem cinco opções de formato oferecidas pelo programador, descritas no quadro, em que “L” e “D” representam, respectivamente, letra maiúscula e dígito.
As letras do alfabeto, entre as 26 possíveis, bem como os dígitos, entre os 10 possíveis, podem se repetir em qualquer das opções. A empresa quer escolher uma opção de formato cujo número de senhas distintas possíveis seja superior ao número esperado de clientes, mas que esse número não seja superior ao dobro do número esperado de clientes.
A opção que mais se adequa às condições da empresa é:
A) I
B) II
C) III
D) IV
E) V
Alternativa E
Calcularemos cada possibilidade na busca daquela que contém como resposta um número entre 1 milhão e 2 milhões. Para facilitar, usaremos notação científica, pois sabemos que:
1 milhão = 106
2 milhões = 2 ⋅ 106
I → LDDDDD
\(26 \cdot 105 = 2,6 \cdot10^6 = 26\cdot 10^5 = 2,6 \cdot 10^6\)
Esse número é maior que 2 milhões, logo, não satisfaz o pedido da empresa.
II → DDDDDD
106 é igual a 1 milhão, logo, não satisfaz o pedido da empresa.
III → LLDDDD
\(262 \cdot 104 = 676 \cdot 10^4 = 6,76 \cdot 10^6 \)
Esse número é maior que 2 milhões, logo, não satisfaz o pedido da empresa.
IV → DDDDD
105 é menor que 1 milhão, logo, não satisfaz o pedido da empresa.
V → LLLDD
\(263 \cdot 102 = 17576 \cdot 10^2 = 1,7576 \cdot 10^6 \)
Esse número está entre 1 milhão e 2 milhões, logo, esse modelo de senha é o ideal.
Fontes
IEZZI, Gelson; MURAKAMI, Carlos. Fundamentos de Matemática Elementar – Volume 5: Combinatória e Probabilidade. 7. ed. São Paulo: Atual, 1998.