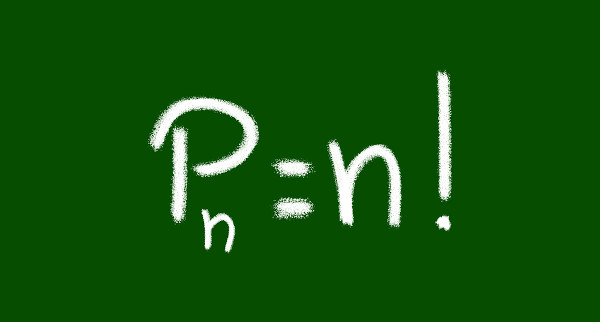A permutação simples é um dos tipos de agrupamentos estudados na análise combinatória. Utilizamo-la para resolver situações-problema do cotidiano. Conhecemos como permutação simples todos os agrupamentos ordenados que podem ser formados com os \(n\) elementos de um conjunto. Para calcular a permutação de \(n\) elementos, representada por \(P_n\), basta calcular o valor de \(n\)!, logo, temos que \(P_n=n\)!.
Saiba mais: Chances de ganhar na Mega-Sena — um cálculo que envolve conceitos de análise combinatória
Tópicos deste artigo
- 1 - Resumo sobre permutação simples
- 2 - O que é permutação simples?
- 3 - Como calcular a permutação simples?
- 4 - Diferença entre permutação simples e permutação com repetição
- 5 - Exercícios resolvidos sobre permutação simples
Resumo sobre permutação simples
- A permutação simples é um tipo de agrupamento estudado na análise combinatória.
- Trata-se de agrupamentos ordenados que são formados utilizando todos os n elementos de um conjunto.
- Para calcular a permutação, utiliza-se a fórmula \(P_n=n\)!
- Existe também a permutação com repetição.
O que é permutação simples?
A permutação simples é um dos agrupamentos estudados na análise combinatória. Trata-se de todos os agrupamentos ordenados que podemos formar com os n elementos de um conjunto. No caso desse tipo de permutação, a ordem é importante.
Exemplo:
Uma fila é composta por 3 pessoas, Amanda, Beatriz e Caio, nessa situação, os 3 podem ser ordenados de 6 maneiras distintas. Quais são elas?
Resolução:
- Amanda, Beatriz e Caio;
- Amanda, Caio e Beatriz;
- Beatriz, Caio e Amanda;
- Beatriz, Amanda e Caio;
- Caio, Amanda e Beatriz;
- Caio, Beatriz e Amanda.
Nesse caso, foram listadas todas as permutações possíveis com esses três elementos. É importante ressaltar que, em uma permutação, a ordem dos elementos é importante, e, como vimos nesse exemplo, temos uma fila e a ordem importa.
Leia também: Arranjo simples — todos os agrupamentos formados com n elementos tomados de k em k
Qual a fórmula da permutação simples?
Para calcular todas as permutações possíveis com determinado conjunto, a permutação de n elementos, representada por \(P_n\), é calculada por:
\(P_n=n!\)
Como calcular a permutação simples?
Para calcular a permutação de um conjunto com n elementos, basta calcular o fatorial do número de elementos, ou seja, n!, e calcular o fatorial de um número é realizar a multiplicação dele pelos seus antecessores.
-
Cálculos de permutação
\(P_2=2!=2\cdot1=2\)
\(P_3=3!=3\cdot2\cdot1=6\)
\(P_4=4!=4\cdot3\cdot2\cdot1=24\)
\(P_5=5!=5\cdot4\cdot3\cdot2\cdot1=120\)
\(P_6=6!=6\cdot5\cdot4\cdot3\cdot2\cdot1=720\)
\(P_7=7!=7\cdot6\cdot5\cdot4\cdot3\cdot2\cdot1=5040\)
Exemplo:
Em uma urna, há 8 bolas de 8 cores distintas, então qual o número de maneiras distintas que podemos retirar essas bolas uma a uma?
Resolução:
Note que, nesse caso, estamos permutando 8 elementos dentro de um conjunto. Calcularemos então a permutação de 8 elementos.
\(P_8=8!=8\cdot7\cdot6\cdot5\cdot4\cdot3\cdot2\cdot1=40.320\)
Diferença entre permutação simples e permutação com repetição
Além da simples, existe a permutação com repetição. A diferença é que, quando temos uma repetição, o total de permutações possíveis será calculado por uma fórmula diferente.
Supondo que nós temos n elementos, e que um deles se repete k1 vezes, o outro k2, e assim sucessivamente, o número de permutações que podemos formar com esses n elementos é calculado por:
\(P_n^{k_1,k_2,\ldots k_j}=\frac{n!}{k_1!\cdot k_2!\cdot\ldots\cdot k_j!}\)
Exemplo:
Quantos anagramas podemos formar com o nome BANANA?
Resolução:
Conhecemos como anagramas todos os reordenamentos possíveis que podemos criar com as letras de uma palavra, logo, estamos calculando permutações. Note que, nesse caso, a letra A se repete 3 vezes e a letra N, 2 vezes, então temos que:
\(P_6^{3,2}=\frac{6!}{3!2!}\)
\(P_6^{3,2}=\frac{6\cdot5\cdot4\cdot3!}{3!2!}\)
\(P_6^{3,2}=\frac{6\cdot5\cdot4}{2!}\)
\(P_6^{3,2}=\frac{120}{2}\)
\(P_6^{3,2}=60\)
Desse modo, há 60 anagramas possíveis.
Exercícios resolvidos sobre permutação simples
Questão 1
Em uma corretora de valores, quando o cliente fica muito tempo sem utilizar o site, para voltar ao uso, é necessário que ele clique nos símbolos & * % $ @ na ordem escolhida durante a criação da conta. Se um funcionário da corretora não sabe a ordem escolhida pelo usuário, tenta descobri-la. Supondo que não haja nenhum bloqueio por erros sucessivos, então o número máximo de tentativas necessárias para desbloquear essa conta é:
A) 5040
B) 720
C) 120
D) 24
E) 6
Resolução:
Alternativa C
Note que há, ao todo, 5 símbolos. Sabendo disso, calcularemos a permutação de 5 elementos.
Então calcularemos \(P_5\):
\(P_5=5!\)
\(P_5=5\cdot4\cdot3\cdot2\cdot1\)
\(P_5=120\)
Desse modo, há 120 maneiras distintas de sequências possíveis para os 5 símbolos.
Questão 2
A Mega-Sena é um jogo composto por um sorteio de 6 números escolhidos entre 60 números. Para ganhar o prêmio máximo, o apostador precisa acertar os 6 números que serão sorteados, independentemente da ordem do sorteio. Ao realizar uma aposta, Pedro escolheu os números 03, 20, 38, 40, 52 e 59, então o número de maneiras distintas que os números escolhidos por Pedro podem ser sorteados, de forma que ele seja o vencedor, é:
A) 120
B) 360
C) 520
D) 720
E) 1040
Resolução:
Alternativa D
Para calcular o total de resultados que torna Pedro vitorioso, basta fazer a permutação de 6 elementos.
\(P_6=6!\)
\(P_6=6\cdot5\cdot4\cdot3\cdot2\cdot1\)
\(P_6=720\)
Por Raul Rodrigues de Oliveira
Professor de Matemática