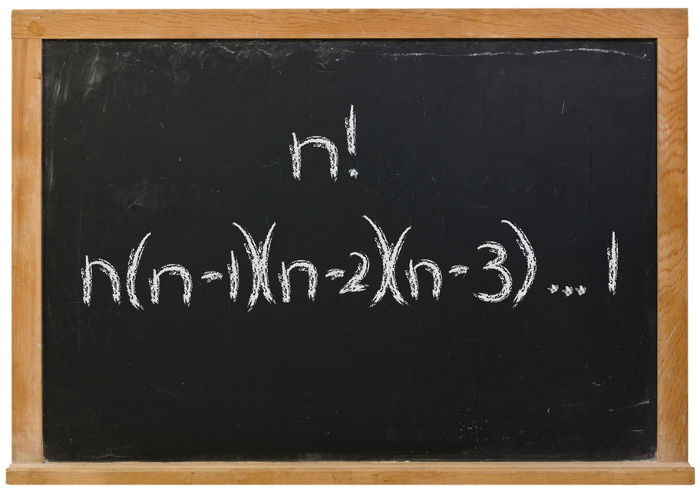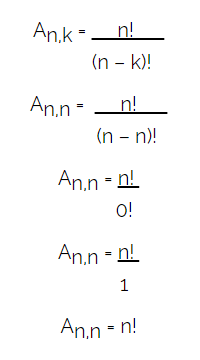O que é permutação?

Permutação é um dos assuntos discutidos na disciplina de análise combinatória em Matemática. Tendo em mãos uma sequência ordenada qualquer com um número “n” de elementos distintos, qualquer outra sequência formada pelos mesmos “n” elementos reordenados é chamada de permutação.

Desse modo, podemos dizer que, se A é uma permutação de B, então A e B são constituídos pelos mesmos elementos, mas ordenados de forma diferente.

Tópicos deste artigo

• 1 - De onde vêm as permutações?
• 2 - Cálculo de arranjos simples
• 3 - Definição de permutação
• 4 - Permutações com elementos repetidos

De onde vêm as permutações?

As permutações são casos isolados dos Arranjos Simples. Estes são agrupamentos ordenados de um conjunto A de elementos, de modo que os grupos possuem um número menor ou igual de elementos do que o conjunto A.

O conjunto A = {X,Y,Z}, {X,Y} e {Y,X} é um arranjo simples dos elementos de A tomados 2 a 2. O número de elementos de A é representado pela letra “n”. O número de ordem, ou número de classe, é “k”. Esse número é a quantidade de elementos de cada arranjo simples (no caso do exemplo, esse número é 2).

A lista com todos os arranjos simples dos três elementos de A tomados 3 a 3 é a seguinte:

XYZ, XZY, ZXY, ZYX, YZX e YXZ

Essa lista é justamente o caso particular dos arranjos que recebe o nome de permutação.

Cálculo de arranjos simples

O número de arranjos simples de um conjunto A, que possui n elementos tomados k a k, pode ser calculado pela seguinte fórmula:

A_n,k =      n!    
         (n – k)!

Definição de permutação

Seja A um conjunto com n elementos distintos. Os arranjos simples desses elementos tomados n a n são chamados de permutações simples de A. Desse modo, para que seja uma permutação, é preciso que o número de ordem k seja igual ao número n de elementos de A. Resulta disso o seguinte cálculo:

Tomando a fórmula utilizada para arranjos simples e o número de ordem k = n, teremos:

Essa é a fórmula utilizada para o cálculo do número de permutações dos elementos do conjunto A, geralmente denotado por P_n. Logo:

P_n = A_n,n = n!

P_n = n!

Exemplo

Calcule o número de permutações das letras da palavra AMOR.

Solução:

Observe que a palavra AMOR tem 4 elementos distintos. Para calcular o número de permutações dessa palavra, utilizaremos a fórmula acima:

P_n = n!

P₄ = 4!

P₄ = 4·3·2·1

P₄ = 24

Portanto, é possível formar 24 permutações diferentes das letras da palavra AMOR. As permutações de palavras também são chamadas de anagramas.

Permutações com elementos repetidos

Um conjunto qualquer pode apresentar elementos repetidos. As permutações desse conjunto devem considerar a repetição desses elementos, pois, a ordem em que eles aparecem não importa, diferentemente da ordem dos outros elementos do conjunto. Se trocarmos apenas os dois “A” de lugar na palavra AMAR, obteremos a mesma palavra. Palavras iguais não são permutações, por isso, essa repetição deve ser subtraída na fórmula para as permutações.

Para subtrair todas as repetições possíveis de elementos em uma permutação com elementos repetidos, devemos fazer o seguinte:

Seja A um conjunto com n elementos, dos quais k elementos repetem-se. A fórmula para o cálculo das permutações de A é:

P_n^k = n!
         k!

Caso o conjunto A, com n elementos, possua k repetições de um elemento e j repetições de outro, o cálculo acontecerá da seguinte maneira:

P_n^k,j =     n!    
          k!·j!

Se um conjunto A, com n elementos, possui k repetições de um elemento, j repetições de outro, … , m repetições de outro, a fórmula assume a seguinte forma:

P_n^k,j,...,m =         n!         
                k!·j!·... ·m!

Exemplo

Calcule o número de anagramas da palavra ANTONIA.

Solução:

Para resolver o exemplo, basta calcular as permutações com elementos repetidos da palavra ANTONIA. Tanto a letra A quanto a letra N repetem-se 2 vezes. Observe:

P₇^2,2 =     7!   
           2!·2!

P₇^2,2 = 7·6·5·4·3·2·1
            2·1·2·1

P₇^2,2 = 5040
           4

P₇^2,2 = 1260

Por Luiz Paulo Moreira
Graduado em Matemática