Fatorial

Calcular o fatorial de um número só faz sentido quando estamos trabalhando com números naturais. Essa operação é bastante comum na análise combinatória, facilitando o cálculo de arranjos, permutações, combinações e demais problemas envolvendo contagem. O fatorial é representado pelo símbolo “!”. Definimos como n! (n fatorial) a multiplicação de n por todos os seus antecessores até chegar em 1. n! = n · (n – 1)· (n – 2) · … · 3 · 2 · 1.

Leia também: Princípio fundamental da contagem – principal conceito da análise combinatória

Tópicos deste artigo

• 1 - O que é fatorial?
• 2 - Cálculo do fatorial
• 3 - Operações com fatorial
• 4 - Simplificação de fatorial
• 5 - Análise combinatória e fatorial
  • Permutação
  • Arranjos
  • Combinação
• 6 - Exercícios resolvidos

O que é fatorial?

O fatorial é uma operação muito importante para o estudo e desenvolvimento da análise combinatória. Na matemática o número seguido do símbolo de exclamação (!) é conhecido como fatorial, por exemplo, x! (x fatorial).

Conhecemos como fatorial de um número natural a multiplicação desse número por seus antecessores com exceção do zero, ou seja:

Vale ressaltar que, para que essa operação faça sentido, n é um número natural, ou seja, não calculamos fatorial de um número negativo, ou mesmo de um número decimal, ou de frações.

Cálculo do fatorial

Para encontrar o fatorial de um número, basta calcular o produto. Note também que o fatorial é uma operação que, ao aumentar o valor de n, o resultado também aumentará muito.

Exemplos:

• 4! =4 · 3 · 2 · 1 = 24

• 5! = 5 · 4 · 3 · 2 · 1= 120

• 6! = 6 · 5 · 4 · 3 · 2 · 1 = 720

• 7! = 7· 6 · 5 · 4 · 3 · 2 · 1 = 5040

Por definição, temos:

0! = 1
1! = 1

Operações com fatorial

Para resolver operações com fatorial, é importante tomar cuidado para não cometer alguns erros. Quando vamos somar, subtrair ou multiplicar dois fatoriais, é necessário calcular cada um deles separadamente. Somente a divisão possui formas específicas para a realização de simplificações. Não cometa o erro de realizar a operação e conservar o fatorial, seja para adição e subtração, seja para multiplicação.

• 2! + 3! ≠ 5!

• 4! · 2! ≠ 12!

• 7! – 5! ≠ 2!

Na hora de resolver qualquer uma dessas operações, devemos calcular cada um dos fatoriais.

Exemplos:

a) 2! + 3! = (2 · 1) + (3 · 2 · 1) = 2 + 6 = 8

b) 4! · 2! = (4 · 3 · 2 · 1) · (2 · 1) = 24 · 2 = 48.

c) 7! - 5! =(7 · 6· 5· 4 · 3 · 2 · 1) - (5· 4 · 3 · 2 · 1) = 5040 – 120 = 4920.

Veja também: Como resolver equação com fatorial?

Simplificação de fatorial

As divisões são bastante recorrentes. Em fórmulas de combinação, arranjo e permutação com repetição, sempre vamos recorrer à simplificação para resolver problemas envolvendo fatorial. Para isso, vamos seguir alguns passos.

Exemplo:

1º passo: identificar o maior dos fatoriais — nesse caso, é 8!. Agora, analisando o denominador, que é 5!, vamos escrever a multiplicação de 8 pelos seus antecessores até chegar a 5!.

O fatorial de um número n, ou seja, n!, pode ser reescrito como a multiplicação de n até k!. Assim,

n! = n·(n -1 ) · ( n- 2 ) · … · k!, logo vamos reescrever 8! como a multiplicação de 8 até 5!.

8! = 8 · 7 · 6 · 5!

Então vamos reescrever a razão como:

2° passo: após reescrever a razão, é possível simplificar o numerador com o denominador, já que 5! está tanto no numerador quanto no denominador. Após a simplificação, basta realizar a multiplicação.

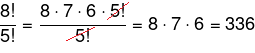
Exemplo 2:

Análise combinatória e fatorial

Ao realizar o estudo mais aprofundado em análise combinatória, o fatorial de um número sempre aparecerá. Os principais agrupamentos da análise combinatória, que são a permutação, a combinação e o arranjo, usam o fatorial de um número em suas fórmulas.

• Permutação

A permutação é a reordenação de todos os elementos de um conjunto. Para calcular uma permutação, nós recorremos ao fatorial, pois a permutação de n elementos é calculada por:

P_n = n!

Exemplo:

Quantos anagramas podemos construir com o nome HEITOR?

Esse é um problema típico de permutação. Como há 6 letras no nome, para calcular a quantidade de anagramas possíveis, basta calcular P₆.

P₆ = 6! = 6 · 5 · 4 · 3 · 2 · 1 = 720

Acesse também: Permutação com elementos repetidos: como resolver?

• Arranjos

Calcular arranjos também exige o domínio do fatorial de um número. Arranjo, assim como a permutação, é a formação de um reordenamento. A diferença é que, no arranjo, estamos reordenando parte do conjunto, ou seja, queremos saber quantos reordenamentos possíveis podemos formar escolhendo uma quantidade k de um conjunto com n elementos.

Exemplo:

Em uma empresa, há 6 candidatos à gestão da instituição, e dois serão selecionados para os cargos de diretor e vice-diretor. Sabendo que eles serão eleitos por votação, qual é a quantidade de resultados possíveis?

Nesse caso, calcularemos o arranjo de 6 tomados de 2 em 2, já que há 6 candidatos para duas vagas.

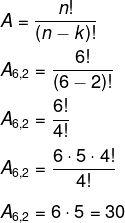
• Combinação

Na combinação, assim como as demais, é necessário o domínio do fatorial de um número. Definimos como combinação os subconjuntos de um conjunto. A diferença é que, na combinação, não se tem um reordenamento, pois a ordem não é importante. Logo, estamos calculando quantos subconjuntos com k elementos podemos formar em um conjunto de n elementos.

Exemplo:

Uma comissão de 3 alunos será escolhida para representar a turma. Sabendo-se que há 5 candidatos, quantas comissões podem ser formadas?

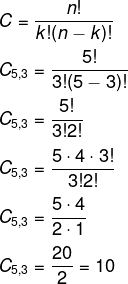
Leia também: Arranjo ou combinação?

Exercícios resolvidos

Questão 1 - Sobre o fatorial de um número, julgue as afirmativas a seguir.

I). 0! + 1! = 2

II). 5! - 3! = 2!

III) 2! · 4! = 8

A) Somente I é verdadeira.

B) Somente II é verdadeira.

C) Somente III é verdadeira.

D) Somente I e II são verdadeiras.

E) Somente II e II são verdadeiras.

Resolução
Alternativa A.

I) Verdadeira.

0! = 1

1! = 1

0! + 1! = 1+1 = 2

II) Falsa.

5! = 5 · 4 · 3 · 2 · 1= 120

3! = 3 · 2 · 1 = 6

5! – 3! = 120 – 6 = 114

III) Falsa.

2! = 2 · 1

4! = 4 · 3 · 2 · 1= 24

Questão 2 - (UFF) O produto 20 · 18 · 16 ·14 … · 6 · 4 · 2 é equivalente a?

A) 20!:2

B) 2·10!

C) 20!:2¹⁰

D) 2¹⁰· 10!

E) 20! : 10!

Resolução

Alternativa D.

Analisando o produto de todos os números pares de 2 até 20, sabemos que:

20 = 2 · 10

18 = 2 · 9

16 = 2 · 8

14 = 2 · 7

12 = 2 · 6

10 = 2 · 5

8 = 2 · 4

6 = 2 · 3

4 = 2 · 2

2 = 2 · 1

Logo, podemos reescrever como 2¹⁰ · 10 · 9 · … ·2 · 1 = 2¹⁰ · 10!

 

Por Raul Rodrigues de Oliveira
Professor de Matemática