Arranjo com repetição

Conhecemos como arranjo com repetição, ou arranjo completo, todos os reagrupamentos ordenados que podemos formar com k elementos de um conjunto com n elementos, sendo que um elemento de n pode aparecer mais de uma vez. A análise combinatória é a área da matemática que desenvolve técnicas de contagem para encontrar a quantidade de possibilidades de agrupamentos em determinadas situações.

Entre esses agrupamentos, está o arranjo com repetição, presente, por exemplo, na criação de senhas, de placas de automóveis, entre outros. Para resolver essas situações, aplicamos como técnica de contagem a fórmula do arranjo com repetição. Existem fórmulas diferentes para calcular o arranjo com repetição e o arranjo sem repetição, então, é importante saber diferenciar cada uma dessas situações para aplicar a técnica de contagem correta.

Leia também: Princípio fundamental da contagem – principal conceito da análise combinatória

Tópicos deste artigo

• 1 - O que é arranjo com repetição?
• 2 - Fórmula do arranjo com repetição
• 3 - Como calcular o número de arranjo com repetição
• 4 - Diferença entre arranjo simples e arranjo com repetição
• 5 - Exercícios resolvidos:

O que é arranjo com repetição?

No nosso cotidiano, deparamo-nos com situações que envolvem sequências e agrupamentos, os quais aparecem ao escolhermos senhas de redes sociais ou de banco, e também em números de telefone ou situações que envolvem filas. Enfim, estamos cercados de situações que envolvem esses agrupamentos.

Por exemplo, nas placas de veículo, que são formadas por três letras e quatro números, existe uma sequência única por estado que identifica cada um dos carros, nesse caso, estamos trabalhando com arranjos. Quando é possível repetir os elementos, estamos trabalhando com o arranjo completo ou arranjo com repetição.

Dado um conjunto com n elementos, conhecemos como arranjo com repetição todos os agrupamentos que podemos formar com k elementos desse conjunto, sendo que um elemento pode se repetir mais de uma vez. Nas placas de veículos, por exemplo, trata-se da quantidade de placas possíveis que podemos formar, levando em consideração que elas possuem três letras e quatro números e que as letras e os números podem se repetir.

Para calcular a quantidade de arranjos com repetição possível, utilizamos uma fórmula bastante simples.

Fórmula do arranjo com repetição

Para encontrar a quantidade de arranjo completo de n elementos distintos tomados de k em

k, em uma determinada situação que admite repetição de um elemento, utilizamos a seguinte fórmula:

AR_n,_k = n^k

AR → arranjo com repetição
n → quantidade de elementos no conjunto
k → quantidade de elementos que serão escolhidos

Veja também: Combinação simples – contagem de todos os subconjuntos de um determinado conjunto

Como calcular o número de arranjo com repetição

Para compreender melhor como aplicar a fórmula de arranjo com repetição, veja o exemplo a seguir.

Exemplo 1:

A senha de um banco possui cinco dígitos formados exclusivamente por números, qual é a quantidade de senhas possíveis?

Sabemos que a senha é uma sequência de cinco dígitos e que não há restrição em relação a repetições, logo, aplicaremos a fórmula do arranjo com repetição. O usuário tem que escolher, entre 10 algarismos, qual vai compor cada um dos cinco dígitos dessa senha, ou seja, queremos calcular o arranjo com repetição de 10 elementos tomados de cinco em cinco.

10^5 = 100.000

Então, há 100 mil possibilidades de senha.

Exemplo 2:

Sabendo que as placas dos veículos são formadas por três letras e quatro números, quantas placas é possível formar?

Nosso alfabeto é composto por 26 letras, e há 10 possibilidades de números, então, vamos separar em dois arranjos completos e encontrar o número de arranjos possíveis para as letras e para os números.

AR_26,3 = 26³ = 17.576
AR₁₀,₄ = 10⁴ = 10.000

Assim, o total de arranjos possíveis é:

17.576 · 10.000 = 1.757.600.000

Diferença entre arranjo simples e arranjo com repetição

Diferenciar o arranjo simples do arranjo com repetição é essencial para a resolução de problemas sobre o tema. O importante para a diferenciação é perceber que, quando estamos lidando com uma situação em que há reagrupamentos cuja ordem é importante, trata-se de um arranjo, e, se esses reagrupamentos admitem repetição entre os termos, trata-se de um arranjo com repetição, conhecido também como arranjo completo. Quando o reagrupamento não admite repetição, trata-se de um arranjo simples.

A fórmula do arranjo simples é diferente da que utilizamos para o arranjo com repetição.

Vimos anteriormente exemplos de arranjo com repetição, agora veja um exemplo de arranjo simples

Exemplo:

Paulo quer colocar em sua estante três dos seus 10 livros escolares, todos distintos entre si, de quantas maneiras ele pode organizar esses livros?

Note que, nesse caso, a ordem é importante, porém não há repetições, tratando-se de um arranjo simples. Para encontrar a quantidade de agrupamentos possíveis, temos que:

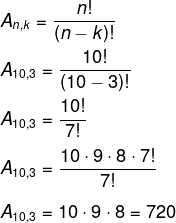
Para saber mais detalhes sobre essa outra forma de agrupamento utilizado na análise combinatória, leia o texto: Arranjo simples.

Exercícios resolvidos:

Questão 1 – (Enem) Um banco solicitou aos seus clientes a criação de uma senha pessoal de seis dígitos, formada somente por algarismos de 0 a 9, para acesso à conta-corrente pela internet. Entretanto, um especialista em sistemas de segurança eletrônica recomendou à direção do banco recadastrar seus usuários, solicitando, para cada um deles, a criação de uma nova senha com seis dígitos, permitindo agora o uso das 26 letras do alfabeto, além dos algarismos de 0 a 9. Nesse novo sistema, cada letra maiúscula era considerada distinta de sua versão minúscula. Além disso, era proibido o uso de outros tipos de caracteres.

Uma forma de avaliar uma alteração no sistema de senhas é a verificação do coeficiente de melhora, que é a razão do novo número de possibilidades de senhas em relação ao antigo. O coeficiente de melhora da alteração recomendada é:

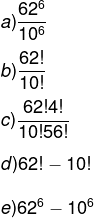
Resolução

Alternativa A

A senha antiga é um arranjo com repetição, como ela pode ser composta por todos os números, então, trata-se de um arranjo com 10 elementos tomados de seis em seis.

AR_10,6 = 10⁶

Já a nova senha pode ser composta pelos 10 algarismos e também por letras maiúsculas (26 letras) e minúsculas (26 letras), então, a senha tem, para cada dígito, um total de 10 + 26 + 26 = 62 possibilidades. Como há seis dígitos, calcularemos o arranjo com repetição de 62 elementos tomados de seis em seis.

AR_62,6 = 62⁶

A razão do novo número de possibilidades de senhas em relação ao antigo é igual a 62⁶/10⁶.

Questão 2 - (Enem 2017) Uma empresa construirá sua página na internet e espera atrair um público de aproximadamente um milhão de clientes. Para acessar essa página, será necessária uma senha com formato a ser definido pela empresa. Existem cinco opções de formato oferecidas pelo programador, descritas no quadro, em que “L” e “D” representam, respectivamente, letra maiúscula e dígito.

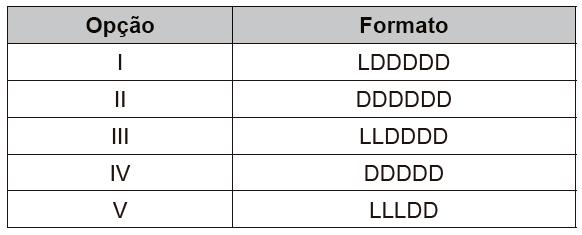
As letras do alfabeto, entre as 26 possíveis, bem como os dígitos, entre os 10 possíveis, podem se repetir em qualquer das opções.

A empresa quer escolher uma opção de formato cujo número de senhas distintas possíveis seja superior ao número esperado de clientes, mas que esse número não seja superior ao dobro do número esperado de clientes.

Resolução

Alternativa E

Calculando cada uma das possibilidades, queremos encontrar a senha que tenha mais que um milhão de possibilidades e menos que dois milhões de possibilidades.

I → LDDDDD

26 ·10⁵ é maior que dois milhões, logo, não satisfaz o pedido da empresa.

II → DDDDDD

10⁶ é igual a um milhão, logo, não satisfaz o pedido da empresa.

III → LLDDDD

26² · 10⁴ é maior que dois milhões, logo, não satisfaz o pedido da empresa.

IV → DDDDD

10⁵ é menor que um milhão, logo, não satisfaz o pedido da empresa.

V → LLLDD

26³ ·10² está entre um milhão e dois milhões, logo, esse modelo de senha é o ideal.

Crédito da imagem

[1] Rafael Berlandi / Shutterstock

Por Raul Rodrigues de Oliveira
Professor de Matemática