O lançamento oblíquo ocorre quando um objeto inicia seu movimento formando um determinado ângulo com a horizontal. Nesse tipo de lançamento, o objeto executa dois movimentos simultâneos, ao mesmo tempo em que executa um movimento na vertical, subindo e descendo, também se desloca horizontalmente.
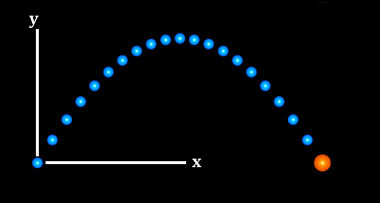
A imagem acima indica a trajetória de um corpo que executa um movimento oblíquo. Esses tipos de movimentos podem ser observados, por exemplo, no tiro de meta executado por um goleiro em uma partida de futebol, e no momento da tacada em uma bola de golfe.
A análise do lançamento oblíquo deve ser feita levando em consideração o movimento executado na vertical (eixo y) e o movimento na horizontal (eixo x). Quanto ao movimento no eixo y, a preocupação será a determinação da altura máxima atingida pelo corpo, por conta da atuação da gravidade neste eixo o movimento será uniformemente variado. As análises do movimento no eixo x irão determinar o alcance horizontal do lançamento, isto é, a distância entre os pontos de partida e chegada. Horizontalmente, o movimento será retilíneo e uniforme.
Tópicos deste artigo
Mapa Mental: Lançamento Oblíquo
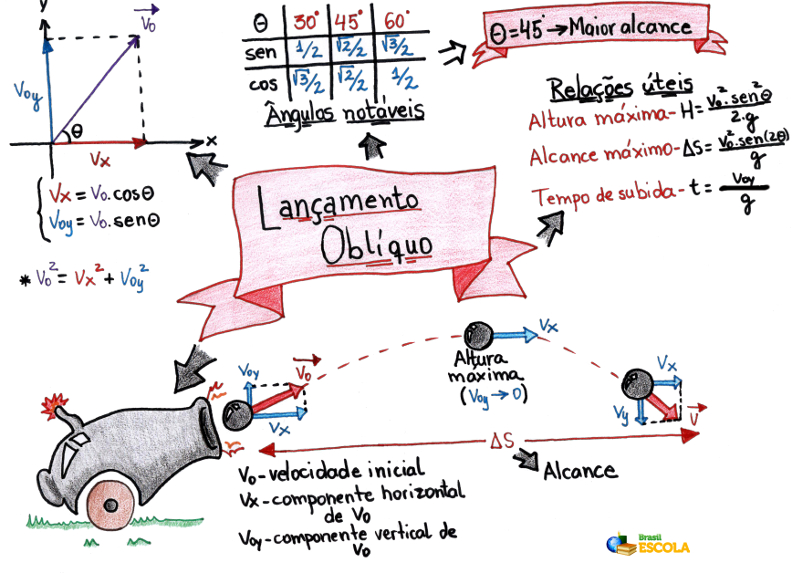
*Baixe o mapa mental sobre lançamento oblíquo!
Alcance horizontal
O alcance horizontal é a distância entre os pontos de partida e chegada do objeto lançado obliquamente. A sua determinação será feita a partir da função horária da posição para o movimento retilíneo uniforme (MRU), sendo assim podemos escrever:
\(s = s_0+V_x\cdot t \rightarrow s-s_0 = V_x\cdot t \rightarrow A = V\cdot cos\theta\cdot t\)
Observe que a diferença entre as posições final (s) e inicial (s0) foi substituída por A, simbolizando o alcance do objeto. Perceba ainda que a velocidade utilizada foi uma componente no eixo x (VX) da velocidade do objeto. A velocidade do objeto forma um ângulo θ com a horizontal, sendo assim, as análises feitas tanto na horizontal quanto na vertical devem utilizar os devidos componentes do vetor velocidade em cada eixo.
Eixo y: Vy = V.sen θ
Eixo x: Vx = V.cos θ
O tempo considerado na equação do alcance (A) é o tempo total para que o objeto saia do chão, atinja a altura máxima e retorne ao solo. No estudo do lançamento vertical, vemos que o tempo gasto para que um objeto atinja a altura máxima vertical é dado por:
\(t_s = \frac{V}{g}\)
Nessa equação, V é a velocidade do objeto e g é a aceleração da gravidade. Para o caso do lançamento oblíquo, a velocidade considerada na vertical será a componente Vy, sendo assim, podemos escrever:
\(t_s = \frac{V_y}{g} \rightarrow t_s = \frac{V\cdot sen \theta}{g}\)
O tempo destacado acima refere-se à subida do objeto, logo, o tempo total do movimento será o dobro.
\(t = \frac{2 \cdot V\cdot sen \theta}{g}\)
Assim, a equação do alcance poderá ser reescrita:
\(A = V\cdot cos\theta\cdot t \rightarrow A = V\cdot cos\theta\cdot \frac{2\cdot V\cdot sen \theta}{g}\\ A = \frac{2\cdot V^2 \cdot cos\theta\cdot sen \theta}{g}\)
O termo 2.cosθ.senθ pode ser substituído pela identidade trigonométrica sen2θ, sendo assim, a equação final para a determinação do alcance horizontal em um lançamento oblíquo será:
\(A = \frac{V^2 \cdot sen 2\theta}{g}\)
O alcance será o máximo possível quando o ângulo de lançamento for igual a 45°. Como o ângulo é multiplicado por dois na equação do alcance, o seno calculado será o de 90°, que corresponde ao máximo valor de seno possível, assim o alcance será o máximo possível.
A imagem abaixo indica as possíveis trajetórias para lançamentos oblíquos executados sobre ângulos diversos. Observe que o maior alcance ocorre quando o ângulo de lançamento é igual a 45º.
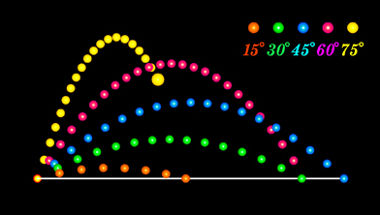
Altura máxima
A altura máxima será determinada a partir da equação de Torricelli, equação do movimento uniformemente variado independente do tempo.
\(V^2 = V_0^2 - 2\cdot a\cdot H\)
Para o lançamento oblíquo, teremos:
\(V_y^2 = V_{0y}^2 - 2\cdot a\cdot H\)
Na altura máxima, a velocidade do móvel será nula. O sinal negativo na equação acima justifica-se pelo fato do movimento ser acendente, contrário ao sentido da gravidade.
\(0 = (V_0\cdot sen\theta)^2 - 2\cdot g\cdot H \rightarrow 2\cdot g\cdot H = V_0^2\cdot sen^2 \theta\)
\(H_{Máx} = \frac{V_0^2\cdot sen^2\theta}{2\cdot g}\)
A equação acima determina a altura máxima atingida por um objeto que executa movimento oblíquo.
Créditos da imagem:
*Mapa Mental por Rafael Helerbrock
Graduado em Física



.gif)