Decomposição vetorial

A decomposição vetorial é uma operação algébrica empregada quando se deseja descobrir a componente horizontal e componente vertical de determinado vetor. Para fazer a decomposição vetorial, precisamos conhecer a posição do vetor original e a posição do ângulo em relação à horizontal ou à vertical.

Leia também: Quais são as operações com vetores?

Tópicos deste artigo

• 1 - Resumo sobre decomposição vetorial
• 2 - O que é um vetor?
• 3 - O que é grandeza vetorial?
• 4 - Para que serve a decomposição vetorial?
• 5 - Como fazer a decomposição vetorial?
• 6 - Exercícios resolvidos sobre decomposição vetorial

Resumo sobre decomposição vetorial

• A decomposição vetorial é usada para descobrirmos a componente horizontal e componente vertical de um vetor.

• Os vetores são segmentos de reta que representam as grandezas vetoriais.

• As grandezas vetoriais são aquelas que precisam ser caracterizadas por meio de um módulo, sentido e direção.

• Para fazer a decomposição vetorial precisamos identificar a posição do vetor para fragmentá-lo em sua componente vertical e horizontal, e identificar se o ângulo está posicionado na horizontal ou na vertical.

• Após a decomposição vetorial, podemos calcular o módulo da componente horizontal, da componente vertical e do vetor que originou as componentes.

O que é um vetor?

Os vetores na Física são segmentos de reta no formato de seta que identificam que uma grandeza física é vetorial; sendo assim, possuem um módulo, direção e sentido.

• Módulo: tamanho, intensidade ou valor numérico da grandeza vetorial, calculado por meio das fórmulas físicas.

• Direção: identifica se a grandeza vetorial está na diagonal, horizontal ou vertical.

• Sentido: identifica se a grandeza vetorial está apontada para a direita, esquerda, norte, sul, leste, oeste, para cima, para baixo, etc.

Para saber mais detalhes sobre vetores, clique aqui.

O que é grandeza vetorial?

As grandezas vetoriais são as grandezas que precisam ser descritas em termos do seu módulo (valor númerico), unidade de medida, direção e sentido. Na Física existem diversas grandezas vetoriais, como a velocidade, deslocamento, aceleração, força e muitas outras.

Para que serve a decomposição vetorial?

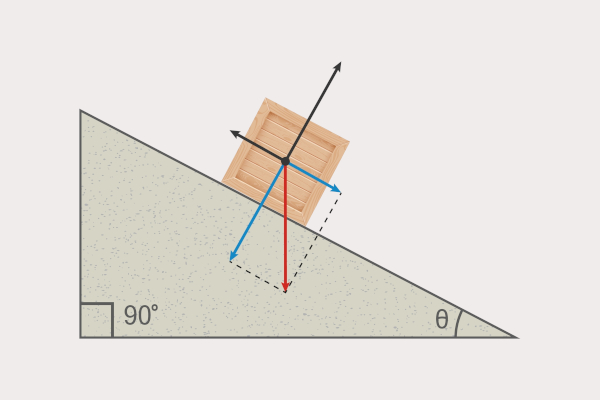
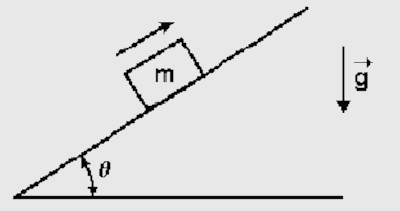
A decomposição vetorial é uma operação algébrica envolvendo vetores frequentemente usada na Física e na Matemática. Por meio dela encontramos as componentes horizontal e vertical de um vetor, também chamadas de projeções ou sombras, servindo para calcularmos os valores das forças em uma situação de equilíbrio ou identificar se as forças estão em equilíbrio em um corpo no plano inclinado, viga, ponto de apoio e muitos outros.

Como fazer a decomposição vetorial?

Para fazer a decomposição vetorial podemos seguir alguns passos:

• Primeiro passo: identificar a posição do vetor para fragmentá-lo em sua componente vertical y e horizontal x.

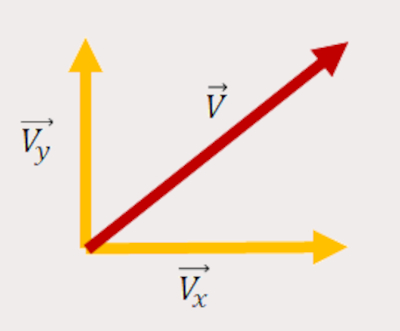
  • Vetor na diagonal para a direita apontando para cima: a componente horizontal está na horizontal para a direita e a componente vertical está na vertical para cima, conforme descrito na imagem abaixo:

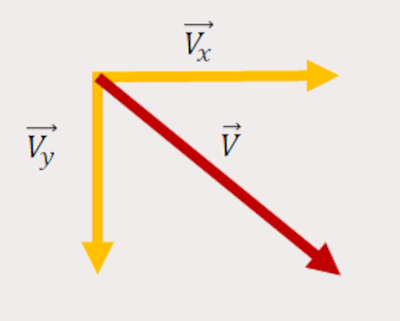
• Vetor na diagonal para a direita apontando para baixo: a componente horizontal está na horizontal para a direita e a componente vertical está na vertical para baixo, conforme descrito na imagem abaixo:

• Vetor na diagonal para a esquerda apontando para cima: a componente horizontal está na horizontal para a esquerda e a componente vertical está na vertical para cima, conforme descrito na imagem abaixo:

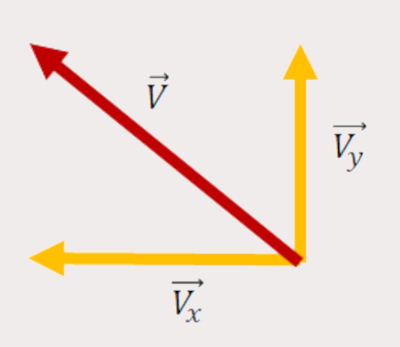
• Vetor na diagonal para a esquerda apontando para baixo: a componente horizontal está na horizontal para a esquerda e a componente vertical está na vertical para baixo, conforme descrito na imagem abaixo:

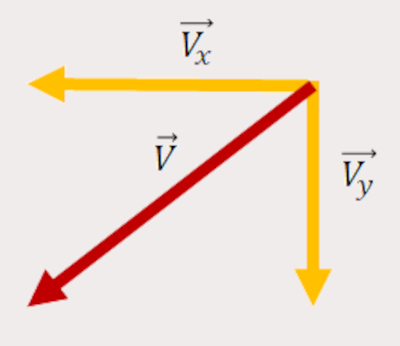
• Segundo passo: identificar se o ângulo está posicionado entre a componente horizontal e o vetor que originou essas componentes (vetor resultante ou vetor original), imagem à sua direita, ou entre a componente vertical e vetor original, imagem à sua esquerda.

• Terceiro passo: calcular o módulo da componente horizontal, componente vertical ou vetor original dependendo do enunciado dos exercícios.
  • Com ângulo na horizontal (entre a componente horizontal e o vetor original), usamos as fórmulas:

\({F}_{x} = F \cdot \cos{\theta} \)

\({F}_{y} = F \cdot \ sen{\theta} \)

• \({F}_{x}\) → componente horizontal do vetor F.
• \({F}_{y}\)→ componente vertical do vetor F.
• \({F} \)→ vetor original.
• \(\cos{\theta} \)→ cosseno do ângulo.
• \(sen{\theta} \)→ seno do ângulo.

• Com ângulo na vertical (entre a componente vertical e vetor original), usamos as fórmulas:

\({F}_{x} = F \cdot \ sen{\theta} \)

\({F}_{y} = F \cdot \ cos{\theta} \)

• \({F}_{x}\) → componente horizontal do vetor F.
• \({F}_{y}\) → componente vertical do vetor F.
• \({F} \) → vetor original.
• \(\cos{\theta} \) → cosseno do ângulo.
• \(sen{\theta} \) → seno do ângulo.

Exemplo

Calcule o tamanho da componente horizontal e da componente vertical de um vetor com orientação nordeste e tamanho de 2 unidades, sabendo que o ângulo formado entre ele e a sua componente horizontal é de 45°. Dados: \(sen 45° = cos 45° = 0,7\).

Resolução:

• Primeiro passo: identificar a posição do vetor e decompor em uma componente horizontal x e uma componente vertical y.

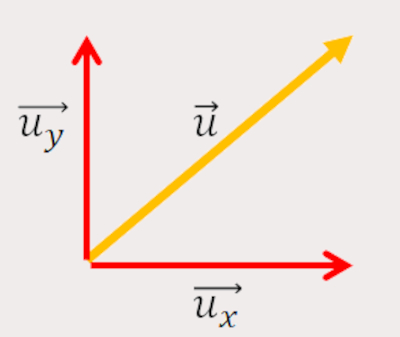
• Segundo passo: identificar a posição do ângulo. Neste caso ele está entre a componente horizontal e o vetor, conforme descrito na imagem abaixo:

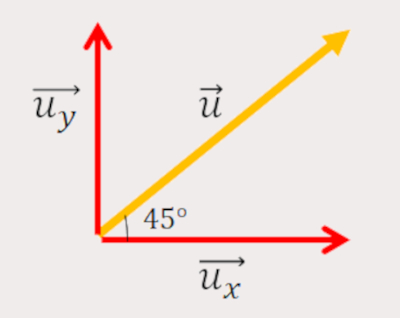
• Terceiro passo: calcular o módulo da componente horizontal, através da fórmula:

\({u}_{x} = u \cdot \cos \theta \)

\({u}_{x} = u \cdot \cos 45^\circ \)

\({u}_{x} = 2 \cdot 0,7 \)

\({u}_{x} = 1,4 \)

E o módulo da componente vertical, através da fórmula:

\({u}_{y} = u \cdot \ sen\theta \)

\({u}_{y} = u \cdot \ sen 45^\circ \)

\({u}_{y} = 2 \cdot 0,7 \)

\({u}_{y} = 1,4 \)

Exercícios resolvidos sobre decomposição vetorial

Questão 1

Calcule a componente horizontal e vertical de um vetor de tamanho 10 m faz um ângulo de 30º com a vertical. Dado sen 30° = 0,5 e cos 30° = 0,9.

A) 4 m e 8 m

B) 5 m e 9 m

C) 6 m e 10 m

D) 7 m e 11 m

E) 8 m e 12 m

Resolução:

Alternativa B.

Como o ângulo está na vertical, entre a componente vertical e o vetor original, podemos calcular a componente horizontal por meio da fórmula:

\({F}_{x} = F \cdot \ sen{\theta} \)

\({F}_{x} = 10 \cdot \ sen{30^\circ} \)

\(F_x = 10 \cdot 0,5\)

\(F_x = 5m\)

E a componente vertical por meio da fórmula:

\({F}_{y} = F \cdot \ cos{\theta} \)

\({F}_{y} = 10 \cdot \ cos{30^\circ} \)

\(F_{y} = 10\cdot {0,9}\)

\(F_{y} = 9m\)

Questão 2

Sabendo que um vetor na diagonal esquerda tem sentido para baixo, qual o sentido da sua componente horizontal e componente vertical?

A) Componente horizontal para a direita e componente vertical para cima

B) Componente horizontal para a esquerda e componente vertical para cima

C) Componente horizontal para a direita e componente vertical para baixo

D) Componente horizontal para a esquerda e componente vertical para baixo

E) Nesse caso não temos componentes horizontal e vertical.

Resolução:

Alternativa D.

Quando temos um vetor na diagonal para a esquerda apontando para baixo, a sua componente horizontal fica acima dele, ou seja, na horizontal apontando para a esquerda. Já a componente vertical fica ao lado direito dele, ou seja, na vertical apontando para baixo.

Fontes

HALLIDAY, David; RESNICK, Robert; WALKER, Jearl. Fundamentos da Física: Mecânica. 8. ed. Rio de Janeiro, RJ: LTC, 2009.

NUSSENZVEIG, Herch Moysés. Curso de física básica: Mecânica (vol. 1). 5 ed. São Paulo: Editora Blucher, 2015.